Pardon my paint skills, I did my best
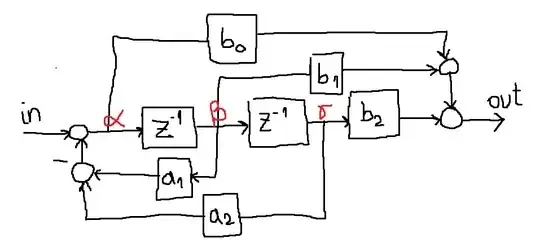
My attempt is short and seems to fail, I have no idea why:
$$\begin{align} \alpha &= in - a_{1}\beta - a_{2}\gamma \\ \beta &= \alpha z^{-1} \\ \gamma &= \beta z^{-1} = \alpha z^{-2} \end{align}$$
inputting 2nd and 3rd equation into the first one I get:
$$\begin{align} \alpha &= in - a_{1}\alpha z^{-1} - a_{2}\alpha z^{-2} \\ in &= \alpha + a_{1}\alpha z^{-1} + a_{2}\alpha z^{-2} \end{align}$$
I can write the output as:
$$\begin{align} out &= b_{2}\gamma + b_{1}\beta + b_{0}\alpha \\ out &= b_{2}\alpha z^{-2} + b_{1}\alpha z^{-1} + b_{0}\alpha \end{align}$$
I have output and input in terms of alpha, but I can't figure what to do from here.