How to deal with a point force acting right on the hinge of a beam?

Question

I have been attempting to solve a question where there is a point force acting on the hinge of a beam. Here is the problem:

I am not sure how to deal with the 2 kN point force at $C$ ($C$ and $E$ are the hinges). If I split the beam into three parts, $\overline{AC}$, $\overline{CE}$, and $\overline{EG}$, I don't know where that 2 kN force should go. If I include it in both of the equilibrium equations of $\overline{AC}$ and $\overline{CE}$, then the sum of $F_y$ will be imbalanced. I believe this problem is statically determinate but I am just stuck at this point. I don't want to attach my workings here yet as I really would like to tackle it myself with a little bit of clarification and help.

Answer 1

I'll assume you know how to find the reactions but you're just unsure of the two hinges at C and E as that seems like your main concern. If you're not sure how to calculate the reactions I can add this later. I have used SkyCiv Beam to find the reactions:

As you can see these reactions balance just fine:

$$\sum F_y = 11 + 10 + 5 - (6+2+6+2\times6) = 26 - 26 = 0\text{ kN} \\ \sum M_A = -32 +6(2)+2(4)+6(5)+12(11)- 10(8) -5(14)= 0\text{ kN.m}$$

Now it doesn't really matter whether you choose to include the 2 kN point load at hinge C on member AC or CE. Just include it in the free body diagram (FBD) for one member or the other (NOT both!).

Let's make the 2 kN point load at C act on the right end of member AC, not the left end of member CE. Remembering that a moment can NOT be supported at the hinge C:

$$\sum F_y = 0\\ 11 - 6 - 2 + H_C = 0\\ \therefore H_C = 3\text{ kN}$$

Now consider member CE (again no moment at C or E). The force Hc needs to be in the opposite direction as that found in the FBD for member AC:

$$\sum F_y = 0\\ H_C + H_E -6 = 0\\ 3 + H_E - 6 = 0\\ \therefore H_E = 3\text{ kN}$$

Lastly consider member EG to confirm that it all balances fine (again the force at E needs to be opposite that in the FBD for member CE):

$$\sum F_y = -H_E + 10 + 5 - 12 = -3 + 10 + 5 - 12 = 0 \text{ }\checkmark$$

Let's look at the shear force diagram (SFD) below and understand why it doesn't really matter which member the 2 kN point load acts on. We solved earlier that at point C the shear force was Hc = 3 kN. As you can see in the SFD there are TWO values at point C (x=4m): 5 kN and 3 kN. Obviously the difference between these values is the 2 kN point load. If we had added the point load in our diagram for member CE instead of member AC then we would have solved the shear force at point C to be Hc = 5 kN. So you can include it in either member and it will be correct - just don't include it in both members.

SkyCiv Beam is pretty handy for analyses like this and it's a good way to check your logic, answers and working out. It will also solve the bending moment diagram (BMD) if you need it plus deflection, stress among others.

Answer 2

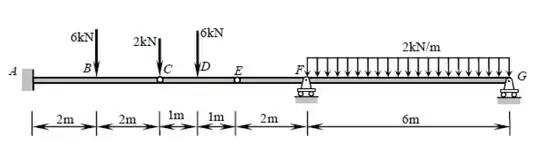
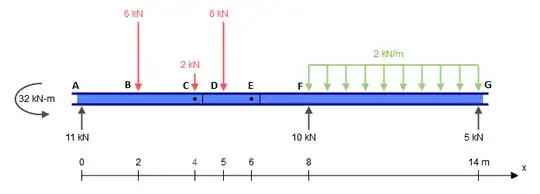
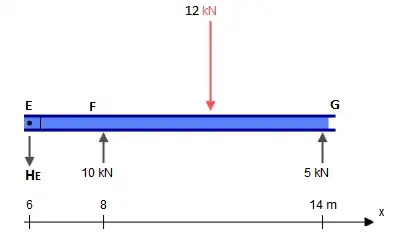
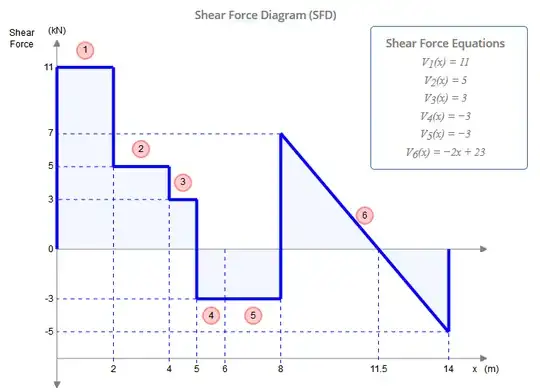
While this beam presents five constraints ($X_A$, $Y_A$, $M_A$, $Y_F$, $Y_G$), it is in fact statically determinate. A statically indeterminate structure is one where there are more unknowns (constraints, in this case) than there are static equilibrium equations. Usually one has three equations: $\sum F_X = 0$, $\sum F_Y = 0$, $\sum M_? = 0$ (where $?$ is any arbitrary point). Hinges, however, give us an additional equation each: $\sum M_{h\pm} = 0$, where $h\hspace{-2pt}\pm$ is one side of the hinge (left or right), such as in this question. This is different from the global null bending moment equation which considers all forces to either side of the hinge. Adding the two additional equations given by the hinges at $C$ and $E$ to the three global equilibrium equations, we therefore have as many equations as we have contraints (5), and can therefore solve this problem by the traditional means.

That being said, there is a much easier way of doing this which is entirely hands-on, without computational aides.

For this hands-on approach, one needs to observe the double hinge in the span $\overline{CE}$. This means that the bending moment at $C$ and $E$ must be null, much like with a simply supported beam (a more in-depth explanation of why this comparison is valid can be seen at the end).

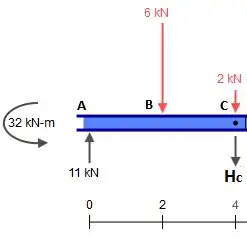
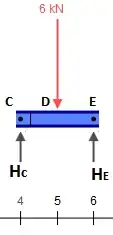
So let's replace that beam with the following pieces (notice that the loads at $C$ and $E$ are left blank for now):

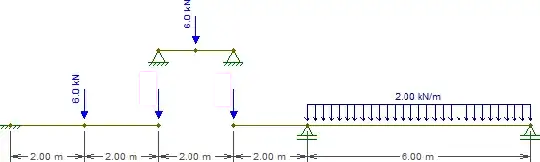
Solving the beam representing $\overline{CE}$ is trivial. For now all we need are the reactions, which are equal to $3\text{kN}$ at each support.

Now get those reactions and toss them down to the other pieces, remembering that at $C$ there is also the concentrated $2\text{kN}$ force, which must be added. We therefore have:

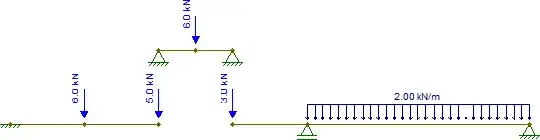
The other pieces are also isostatic and can be trivially solved (assuming one knows how to obtain internal forces of isostatic structures). The resulting internal forces are (I changed the support at $G$ just to make that piece stable for horizontal forces, which changes nothing in this case):

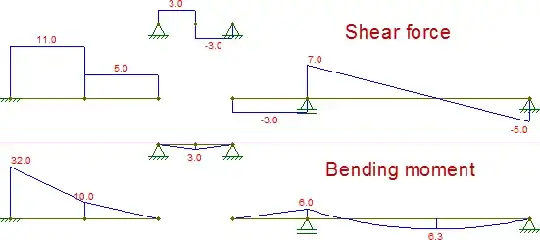
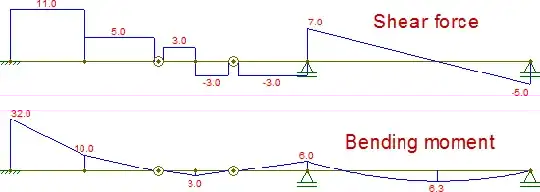
Composing these diagrams, they are identical to those obtained by the original beam:

A simple reason why the comparison can be made between those double-hinges and a simply supported beam is because this is the basic principle behind Gerber beams (which is basically what $\overline{CE}$ represents). They are beams which rest on other beams (see example here, where the beams to the right and left are Gerber beams) and which can therefore be "lifted" from the rest of the structure, solved, and then have their reactions distributed to the rest of the structure. One doesn't have to worry about the influence of external forces or the neighboring beams transmitting shear forces due to the fact that the bending moment must be null at each extremity of the Gerber beam. This means that the integral of the shear along the Gerber beam must be null, which can only occur if only the loads within the beam and the reactions at its extremities are considered.

The program I used for these diagrams was Ftool, a free 2-D frame analysis tool.