Calculating the bending moment ($M$) of a beam as it relates to stress ($σ$) and strain ($ε$)?

Question

I am trying to learn how to work out the bending moment for progressively complex systems to model a beam. I am assuming only one axis of motion (transverse = $y$).

For the basic equation of material elasticity, $σ$ represents stress and $ε$ represents strain in terms of longitudinal stretch of each segment of the beam resulting from transverse ($y$) displacement.

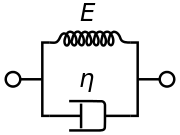
(1) Simple Spring

If you model the beam as a simple spring for which $E$ (Young's Modulus) is the spring constant and $I$ is the cross-sectional moment of inertia, according to this reference, you get an equation of material elasticity and bending moment, respectively, as:

$σ = Eε$

$M = EIy_{xx}$

According to Wikipedia though, it's the following, so I'm not sure about signs:

$M = -EIy_{xx}$

(2) Damped Spring

If you add a damper to the bar simulation, according to this reference, you get the following:

$σ= Eϵ-ηε_t$

$M=-EIy_{xx}-Iηy_{xxt}$

Question

I am having trouble understanding how to extrapolate these principles to increasingly complex beam models.

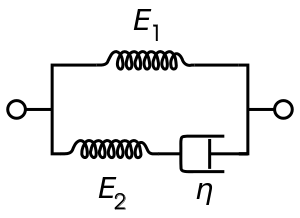
Three Element System:

For example, in a three element model you can have:

$σ + \frac{η}{E_2}\dot{σ} = E_1ε + \frac{η(E_1+E_2)}{E_2}\dot{ε}$

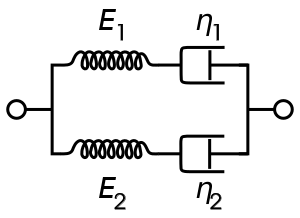
Four Element System:

Or in a four element model you might have:

$σ + (\frac{η_1}{E_1} + \frac{η_2}{E_2})\dot{σ} + \frac{η_1η_2}{E_1E_2}\ddot{σ} = (η_1+η_2)\dot{ε} + \frac{η_1η_2(E_1+E_2)}{E_1E_2}\ddot{ε}$

How would you similarly go about expressing the bending moment with these types of more complex models?

My Guess

From looking at the two known equations above, except for the signs which I don't know how to anticipate, it looks like the equation for the bending moment can be defined somewhat as follows.

Two Element System:

$σ= Eε-η\dot{ε}$

$M=-EIy_{xx}-Iηy_{xxt}$

$M = -I(σ_{bend})$ (which roughly matches this ref)

$σ_{bend}= Eε_{bend}-η\dot{ε}_{bend}$

$ϵ_{bend} = y_{xx}$

Three Element System:

If so then for the three element system we might have:

$σ_{bend} + \frac{η}{E_2}\dot{σ_{bend}} = E_1ε_{bend} + \frac{η(E_1+E_2)}{E_2}\dot{ε_{bend}}$

$M = E_1Iy_{xx} + I\frac{η(E_1+E_2)}{E_2}y_{xxt} - \frac{η}{E_2}\dot{M}$

Is this the right idea? What do you do with signs here? It seems like the signs don't match to the equations of motion in the two given examples so I'm not sure if there's something more to be done with them.

Thanks for any help.

Answer 1

To address sign convention: It is not uncommon to consider bending stress as negative with respect to beams because loads are typically acting downwards. However; your equations for bending stress is foreign to me and seems incorrect. Bending stress, for prismatic beams, is typically represented as $\sigma=\frac{Mc}{I}$ where $M$ is the bending moment, $c$ is the distance to the neutral axis, and $I$ is the second area moment of inertia.

If you wanted to put this in terms of strain and the elastic modulus it would become: $\epsilon E=\frac{Mc}{I}$; provided you do not exceed the proportional limit of the material. You could then draw the conclusion that $\epsilon/c$ is equivalent to the curvature of the beam under load, $1/\rho$. This gives us the classic relationship between curvature, mechanical property and applied load: $$\frac{1}{\rho}=\frac{M}{EI} \tag{1}$$

Before moving to more complicated beams, I would make sure to understand this concept. Additionally, I'll note that this only applies for relatively small displacements (a topic for another time), but this boundary conditions is how we go from $(1)$ to: $$\frac{d^2\upsilon}{dx^2}=\frac{M}{EI}\tag{2}$$

Regarding treating $E$ as the materials' spring constant, the units are wrong. Spring Constants have units of $\frac{load}{length}$, whereas $E$ has units of $\frac{load}{length^2}$. For example, in imperial units: $\frac{lbs.}{in^2}$. To determine the spring constant of a beam, you need to make the units work and to do so, you may end up with something like this: $$k=\frac{EA}{L}\tag{3}$$

Considering your images, the "beam" would only defect so far as the spring allows or $\upsilon=\frac{F}{k}$. If it were to deflect less, or more, then you could use a simple free body diagram to solve your problem given that you know the boundary conditions at the maximum and minimum spring deflection. I recommend a copy of Shigley's Mechanical Engineering design for good examples of this.

I might have assumed that since you are considering dampers, that you are concerned with spring back. In this case, the damper would work against the potential energy of the spring. Although, it does appear that your dampers are in series with your springs. Either way, you're missing some information to solve that dynamic damper problem, namely velocity; which I suppose you could solve for if the forces and material properties were known.