Required force to start the motion of a leaning bar

Question

A uniform bar weighing 343N leans on a heightened plane (see figure). What force P is needed to start the bar moving?

Coefficient of friction (on all surfaces) = 0.30

The blurred length is most probably 5m.

I've done several revisions on answering this problem: adding a vertical friction force on the edge, adding another one to the horizontal of the edge, considering the weight on the other end of the bar, putting the weight at the midpoint of the bar, etc.

It's kind of tricky, that my equations did't add up — different answers on different equations of the same variables.

The given answer is: P = 246N

~ Problem solved. Turns out I just had to put the bar on the horizontal, and get the component of every force thereafter. Problems with triangles can get confusing.

Answer 1

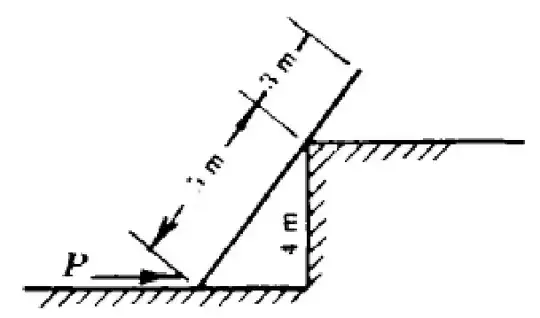
This is a diagram of the reaction forces at points A and B. The reaction forces are perpendicular to the surface of contact for A. In the case of B, again the reaction force is perpendicular to a surface (think of it the reaction).

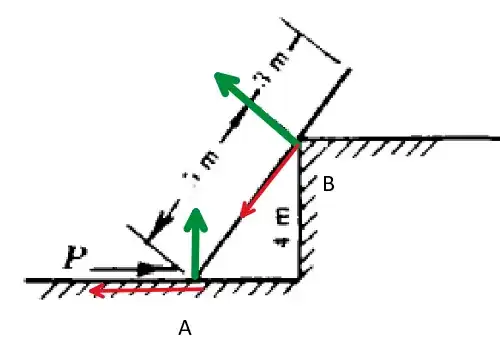
So you have the following forces:

• $N_A$: reaction force at point A
• $T_A$: Friction force at point A
• $N_B$: reaction force at point B $\left(\frac{N_{By}}{N_B{x}}=\frac{3}{4}\right)$
• $T_B$: Friction force at point B $\left(\frac{T_{By}}{T_B{x}}=\frac{-4}{3}\right)$

Regarding the friction forces they are drawn this way, because that will be direction of force when the force P is large enough for them to start moving. Additionally, the magnitude of the friction forces will be (just before movement is initiated):

$$T_A = \mu N_A, \quad T_B=\mu N_B$$

In order to calculate $N_B$ we can estimate by the equilibrium of moments about point A:

$$\sum M_A = 0 \rightarrow N_B\cdot 5m - W\cdot \left(4\cdot\frac{3}{5}\right) = 0$$

Where:

• W is the weight of the bar and its applier right at the middle of the beam (4[m] from the edge). The horizontal distance from point A is $\left(4\cdot\frac{3}{5}\right)$

$$N_B = \frac{12}{25}\cdot W$$

The equilibrium of forces on Y axis is:

$$\sum F_y = 0 \rightarrow N_A + N_{By} -T_{By}-W = 0 $$ $$N_A + N_{B}\frac{3}{5} - \mu\cdot N_{B}\cdot \frac{4}{5} -W = 0 $$ $$N_A + \frac{12}{25}\cdot W(\frac{3}{5}- \mu\cdot \frac{4}{5}) -W = 0 $$ $$N_A =\left(1 + \frac{12}{25}(\mu\cdot \frac{4}{5}-\frac{3}{5} \right)\cdot W $$ $$N_A =\frac{517}{625}\cdot W $$

In order to calculate $P$ we can estimate by the equilibrium of moments about point B:

$$\sum M_B = 0 \rightarrow -N_A\cdot 3m + (P- T_A)\cdot 4m + W\cdot \left(1\cdot\frac{3}{5}\right) = 0$$

$$ P=\frac{1}{4}\left(N_A\cdot 3m - W\cdot \left(1\cdot\frac{3}{5}\right) \right) +T_A$$

$$ P=\frac{1}{4}\left(\frac{517}{625}\cdot W\cdot 3m - W\cdot \left(1\cdot\frac{3}{5}\right) \right) +\mu \cdot \frac{517}{625}\cdot W$$

$$ P=\left(\frac{1}{4}\left(\frac{517}{625}\cdot 3 - \frac{3}{5}\right) +\mu \cdot \frac{517}{625}\right)\cdot W$$

$$ P=\frac{4491}{6250} \cdot W$$