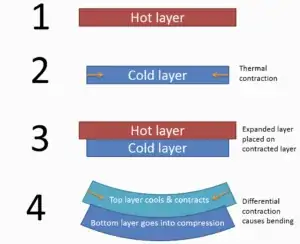
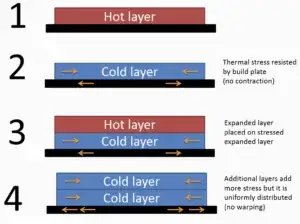
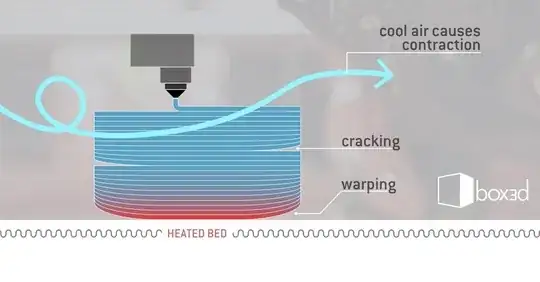
3D printed parts cool down during printing, resulting in thermal contraction which causes a bending moment and separation from the printing bed.
The issue is solved by increasing adhesion to the printing bed, which however results in more stresses inside the part which can cause cracking.
The result is a poor printed part:
Provided I know the thermal expansion coefficient of a material and the Young modulus, the temperature delta causing contraction (which should be glass transition temperature minus ambient temperature) and the part length, how can I calculate the adhesion force required to keep the corners of the part sticking to the bed, or the adhesion force required to keep the layers together, without delamination?
I know that complex shapes would require different calculation. For this question I would consider only parallelepipeds ("boxes", "beams").
It may be dependent on layer height, but I think it can be regarded as second order parameter and omitted from a rough estimate.
An approximation is enough, I guess that accurate results would require a finite element analysis, which is beyond the scope of this question.
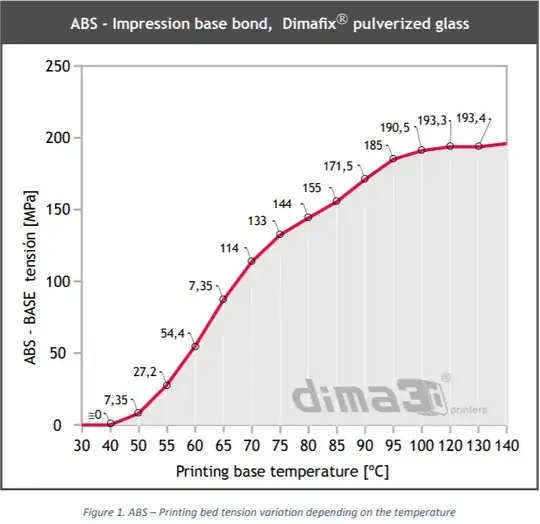
For reference, the available adhesion force provided by a specific product (Dimafix) is the following, as shown in their report: