Hello all of you engineering geniuses. Awhile ago a very talented individual on here helped me work out the conceptual mechanics of this design. As you can see from the model, there is a lead screw assembly that pushes a rod forward which elevates the platform. The total travel is 0° to 60° (theta). The equation shown is the linear travel of "Xblock" as a function of theta. If you were to plot this function, you will see it is not quite linear. The terms, Wp, Ht, Hp, and Lrod are all constants. I am trying to determine an equation for angular velocity of the platform, which is actually decelerating as Xblock moves forward at a constant velocity. Of course the linear travel is easy enough, simply the rps of the motor x lead x time. The lead is 8mm but the lead and rps can be treated as constants. I could simply take the derivative of function, but it's a function of position as a function of another position, not time, so I'm not entirely sure where to go from here. 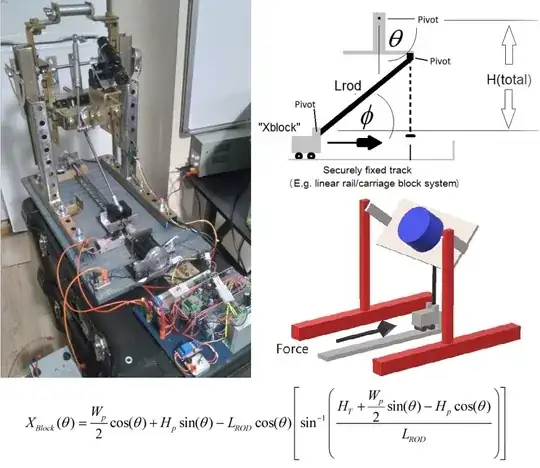
- 35
- 5
1 Answers
As PeteW mentioned you can differentiate both sides of the equation with respect to t, and then solve for $\dot\theta(t)$.
If I done correct the calculations, you'll end up with
$$\dot\theta(t) = -\frac{X'(t)}{a(\theta(t)) + b(\theta(t))}$$
where:
- $a(\theta(t))= -H_{p} \cos(\theta(t))+ \frac{1}{2} W_{P} \sin(\theta(t))-L_{rod} \arcsin\left(\frac{H_T-H_{p} \cos(\theta(t))+\frac{1}{2} W_{P} \sin(\theta(t))}{L_{rod}}\right) \sin(\theta(t)) $
- $b(\theta(t))= \frac{\cos(\theta(t))}{\sqrt{1-\frac{\left(H_T-H_{p} \cos(\theta(t))+ \frac{1}{2} W_{P} \sin(\theta(t))\right)^2}{L_{rod}^2}}} \left(\frac{W_{P}}{2} \cos(\theta(t))+H_{p} \sin(\theta(t))\right)$
- $X'(t)=\frac{2\pi n}{60} l_{thread}$: the velocity of the cart:
- $n$ is the revolutions per minute [rpm]
- $l_{thread}=8[mm]$ is the thtread size in [meters]
After, all the simplifications the angular velocity can be calculated as a function of $n [rpm]$, and $\theta [rad]$
$$\dot\theta(n, \theta) = -\frac{2\pi l_{thread}}{60(a(\theta) + b(\theta))}n$$
where:
$a(\theta)= -H_{p} \cos(\theta)+ \frac{1}{2} W_{P} \sin(\theta)-L_{rod} \arcsin\left(\frac{H_T-H_{p} \cos(\theta)+\frac{1}{2} W_{P} \sin(\theta)}{L_{rod}}\right) \sin(\theta) $
$b(\theta)= \frac{\cos(\theta)}{\sqrt{1-\frac{\left(H_T-H_{p} \cos(\theta)+ \frac{1}{2} W_{P} \sin(\theta(t))\right)^2}{L_{rod}^2}}} \left(\frac{W_{P}}{2}\cos(\theta)+H_{p} \sin(\theta)\right)$
- 24,340
- 3
- 38
- 77