In order to assess the efficiency you need to compare the heat transfer rate $\dot{Q}$ with and without blinds. There are a few studies comparing the effect of blinds (internal/external/enclosed) on heat transfer. One of them in 2014 Effect of the roller blinds on heat losses through a double-glazing window during heating season in Central Europe, found energy saving of about 33% for internal blinds during the night and 45% for external blinds. (Notice that in order to simplify the calculation they are stating night time).
So in order to calculate the savings you need to be able to calculate the heat transfer of a window.
heat transfer of a window
The actual heat transfer has the following temperature profile:
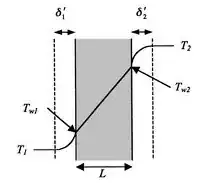
In this scenario
- $T_1= -12.5[^oC]$, (9 Fahrneit ) and
- $T_2= 17.5[^oC]~ \approx 63.5[F]$ (inside temp)
the temperature differense $\Delta T = 30[^oC] $
A typical double glazing window has a U value of $2.8 \left[\frac{W}{m^2 K}\right]$.
Additionally you can estimate that the convective coefficient of transfer is
- $h_o = 20\left[\frac{W}{m^2 K}\right]$
- $h_i = 8 \left[\frac{W}{m^2 K}\right]$
Then the thermal resistance of the wall is:
$$R_{total} = R_{out} + R_{windows}+ R_{in}$$
$$R_{total} = \frac{1}{h_o A} + \frac{1}{U_{window} A}+ \frac{1}{h_i A}$$
where A is the window area. This can be simplified to
$$R_{total} = \frac{1}{ A}\left(\frac{1}{h_o } + \frac{1}{U_{window}}+ \frac{1}{h_i}\right)$$
And the total heat tranafer rate is equal given by:
$$\dot{Q} = \frac{T_2-T_1}{R_{total}}$$
$$\dot{Q} = \frac{T_2-T_1}{\frac{1}{ A}\left(\frac{1}{h_o } + \frac{1}{U_{window}}+ \frac{1}{h_i}\right)}$$
$$\frac{\dot{Q}}{ A} = \frac{T_2-T_1}{\left(\frac{1}{h_o } + \frac{1}{U_{window}}+ \frac{1}{h_i}\right)}$$
if you substitute the numbers in you get
$$\frac{\dot{Q}}{ A} \approx = 56 \left[\frac{W}{m^2}\right]$$
energy saving compared to LED
Based on the article that means that during the night you get an energy saving of about $$0.33\cdot 56\left[\frac{W}{m^2}\right]\approx 19\left[\frac{W}{m^2}\right]$$
Assuming you have a window opening of about 1$[m^2]$, the savings are about 1.5 times greater that LED.
Obviously, the savings will be :
- greater if the window is bigger
- less as temperature difference get smaller
Radiative heat transfer
The main factor that is of consideration here is the solar radiation. There are three types of radiation:
- Direct radiation: the direct rays of the sun. (this is zero on a cloudy day).
- Diffuse radiation: this is always present and its an effect of the presence of atmosphere. In higher latitudes it tends to increase because the sun rays need to "pass through" more atmosphere.
- reflected (you can neglect this)
If you can get the rays of the sun (direct radiation) into the house, this will always be a significant plus in the heat balance of the house.
Final thoughts
This problem is very instance specific depending on:
- the location of the house
- orientation of windows
- type of blinds, etc.
Therefore, it is impossible to draw a generic conclusion. As such, only trends can be realistically observed.
At a temperature difference of 30$[^oC]$ it makes sense to close the blinds on a cloudy day. However, if you get closer to 15$[^oC]$ then the savings are diminished.
If the windows are positioned in the right angle and light shines into the room, then expect the added solar radiation will improve the heat balance in favour of open blinds.
