Unbraced Length for Lateral Torsional Buckling vs. Yield Strength

Question

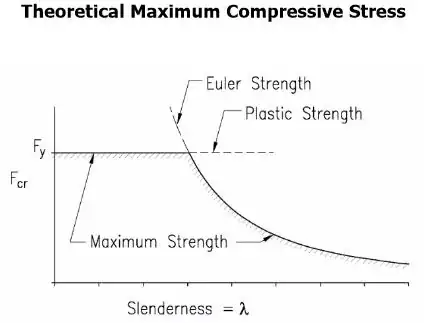
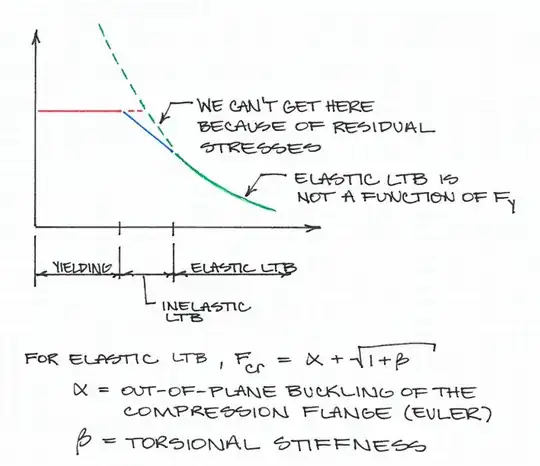
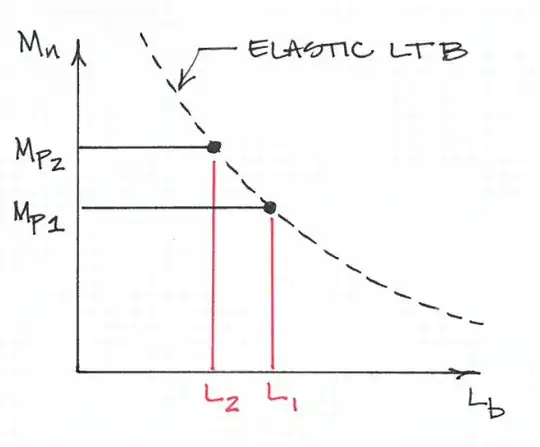
The AISC 360-10 Specification for Structural Steel Buildings gives provisions for calculating the maximum unbraced length of a compression flange that separates yielding moment from lateral torsional buckling (LTB). This formula is (AISC 360-10, Eqn. F2-5):

$$ L_p = 1.76r_y\sqrt{\frac{E}{F_y}} $$

where

$L_p =$ limiting length that separates full yield moment and LTB
$r_y =$ radius of gyration about the $y$-axis
$E =$ Young's modulus
$F_y =$ yield strength of material

Assuming that one is using regular structural steel, the Young's modulus of the material is assumed to be the same regardless of steel grade.

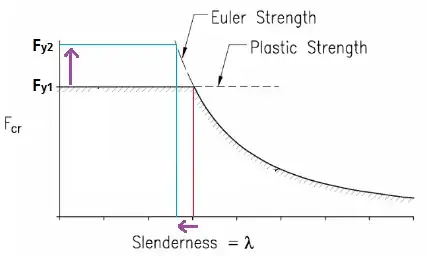
This equation works out such that a steel with a lower yield strength may actually be braced at a lesser interval than one with a higher yield strength. In other words, given the same beam size, the material with the higher yield strength buckles first.

I have also found this to be applicable to design using the ASME Boiler & Pressure Vessel code, specifically Division III, Subsection NF for supports. With temperature effects on yield strength and Young's modulus taken into account, it's possible that a member at an elevated temperature may buckle at a longer length than one at room temperature.

This seems counter-intuitive to me. Why would a weaker material exhibit less LTB action with the same given length?

Answer 1

Slenderness ($\lambda = L/r$) is the ratio of a member's length to its smallest radius of gyration. It should make sense that:

• The less slender a member, the more its plastic strength needs to be considered rather than its Euler (buckling) strength.
• The more slender a member, the more its Euler (buckling) strength needs to be considered rather than its plastic strength.

In other words as slenderness increases there becomes a point where critical buckling stress becomes the limiting factor rather than plastic yield strength ($F_y$). The maximum allowed compressive strength is the minimum of yield strength and buckling strength. This is illustrated in the diagram below:

$$ \lambda = L_p/r_y = 1.76\sqrt{\frac{E}{F_y}} $$

The formula you have provided has separated yielding moment from lateral torsional buckling (LTB) as you stated. This would be the slenderness point where the critical strength changes from the plastic strength to the Euler strength. If $F_y$ increases, then this point on the x-axis would move to the left. This means slenderness $\lambda$ would be smaller and hence the length of the member (or length between bracing points), $L$ should be smaller.

Looking at the formula it does seem counter-intuitive. But what you have to remember is that it's either going to fail due to plastic yielding or LTB. And so at higher yield strengths, the buckling strength falls below the yield strength at lower slenderness (smaller member length) than lower yield strengths.

Hope that helps.

Answer 2

As discussed in the earlier answer, if we look at the curve of moment capacity versus unbraced length we see three regions of behavior -- yielding, inelastic LTB, and elastic LTB (see Fig. C-F1.1 in the AISC Steel Construction Manual). It is important to note that we only have inelastic LTB due to residual stresses. This is where that $0.7F_yS_x$ term is coming from (residual stresses are assumed to be $0.3F_y$). It is also important to note that the equation for critical stress at elastic LTB is in the form $\alpha + \sqrt{1+\beta}$ and is not a function of yield stress. Alpha is a term for out-of-plane buckling of the compression flange and beta is a term for torsional stiffness.

So, conceptually, we could look at a curve that disregards residual stresses - meaning we have just yielding and elastic LTB. When we increase $F_y$, the elastic LTB curve remains the same while $M_p$ increases. The result is that we transition to elastic LTB at a smaller unbraced length. One way to think about it is that with an increased $F_y$, it takes more force to yield the member, making it more likely that it will buckle before yielding.