Modeling Vehicle Acceleration - Simulink

Question

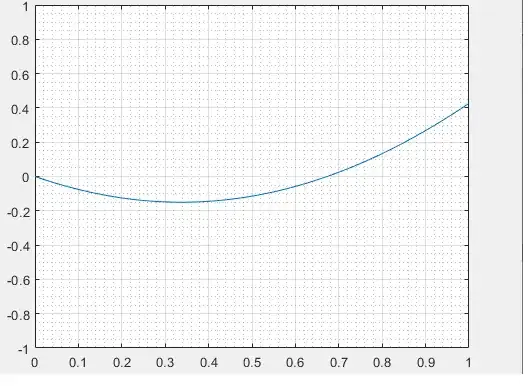
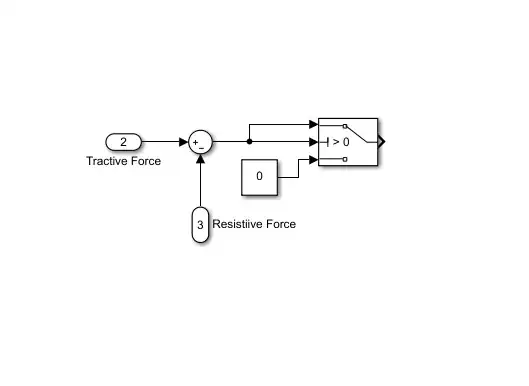
Hello I am modeling a vehicle that has a seperately excited DC motor as the power plant utilizing the constant-torque and constant-power regions for traction. The acceleration is governed by the following equation $$ M \frac{dv}{dt} = F_t -(\beta_1+\beta_2v^{2}+\beta_3v) $$

The problem with my model is that the $\beta_1$ component, the rolling resistance, is a constant value and causes the velocity to go negative for the first 0.7 seconds when the model is executed . Any suggestion on how to fix this issue?

Answer 1

If this is the case, the equation either needs a domain readjustment(so, valid from t∈[0.7,∞]) or an equation redefinition.

Using a piecewise function would look like: $$ M \frac{dv}{dt} = F_t -(\beta_1+\beta_2v^{2}+\beta_3v), t∈[0.7,∞] $$ $$ M \frac{dv}{dt} = 0, t∈(0,0.7) $$

Friction, is just a reactionary force. For rolling resistance can be modelled as an example of a dynamic friction. Hence, until motion occurs, $$F_t = β_1$$ Then, you should get better looking profiles.

Another way to do this would be to have a criteria, where the reactionary $β_1$ is just as big as $F_t$.

Therefore, $$ M \frac{dv}{dt} = F_t -(\beta_1+\beta_2v^{2}+\beta_3v), t∈[0,∞] $$ Where $$ \beta_1 =F_t, F_t∈[0,\beta_{max}] $$ $$ \beta_1 =\beta_{max}, F_t∈[\beta_{max},∞] $$

Here, $\beta_{max} $ is your initial value of $\beta_1$

Answer 2

I solved the issue with a switch function block, it not the best solution but it works for my basic simulation. Thanks again