Can strength be expressed in a single value? Can flexibility?

Question

I'm trying to communicate information about the strength and flexibility of certain materials to laymen. Are there any recognised proxies for strength and flexibility?

I've tried:

$$\text{Strength Proxy} = \sqrt {\text{Tensile Strength} * \text{Flexural Strength)}}$$

and

$$\text{Flex Proxy} = \frac{1}{\sqrt{\text{Tensile Modulus} * \text{Flexural Modulus}}}$$

My plan was to normalise the distribution and give some value from 1-10 for each material but the above formulae gave some results that didn't make sense.

However this is defined it will be imperfect. Therefore I am just looking for a systematic way to make a first approximation.

Answer 1

Another way to approach is to determine the properties that influence the specific problem at hand. I'll give an example and you can see if it works for you.

Define the problem.

Lets assume that you want to determine the most appropriate material for the tensile testing of a bar of length L (with a uniform cross-section), and safety factor N, so that the weight of the bar is minimum.

From this problem you have the following specifications:

• Geometric
  • Length L
• Material
  • $\rho$ material density
  • $\sigma_{UTS}$ material strength
• Functional requirements
  • F: maximum tensile force
  • $N$: safety factor.

Determine the crucial parameter

The mass of the material is given by $m = \rho \cdot L\cdot A$

The cross-sectional area A required to transfer the force will be given by:

$$A = \frac{F\cdot N }{\sigma_{UTS}}$$

Substituting, A to the mass equation you obtain

$$m = \rho \cdot L\cdot \frac{F\cdot N }{\sigma_{UTS}}$$

Now you can rearrange the formula as follows

$$m=\underbrace{F\cdot N}_{\text{Functional}} \cdot \underbrace{L}_{\text{Geometry }} \cdot \underbrace{\frac{\rho}{\sigma_{UTS}}}_{\text{material}}$$

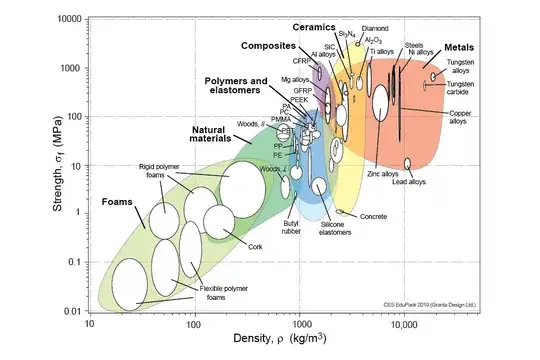
From this you can see that in order to minimise the mass for this type of loading you need to minimise the ratio $\frac{\rho}{\sigma_{UTS}}$ or equivalently maximise the ratio $\frac{\sigma_{UTS}}{\rho}$.

Then you can look for Ashby diagrams for Strength - density and find out which material is the most appropriate.

Other examples

You can follow the same pattern and you can for example:

• Determine the material properties to minimise the deflection given a specific mass.

In that case you would end up with material index $\frac{E}{\rho}$. Again you would look for an Ashby diagram for Stiffness - Density and select the most appropriate material

• Determine the material properties to minimise the cost of the material for a given deflection.

In that case you would end up with material index $\frac{E}{\rho\cdot C_m}$ (where $C_m$ is the material cost per kilo). Again you would look for an Ashby diagram for Stiffness - Density and select the most appropriate material

• Other loading conditions:

Things become more interesting when you consider buckling, bending or torsion.

final thoughts

Obviously this is tailor made to the application you have in mind. Therefore you are required to do some work depending on your problem. However, it is arguably a good starting point to categorize the materials based on the specific parameters of the problem at hand.

Of course, there are other parameters like workability, corrosion, toxicity that will remove some candidates, that need to be considered.

Answer 2

The young's modulus (E) is the best indicator of material strength. In terms of rigidness and flexibleness of a structure of certain material, you need to relate E to the deformation behavior and geometric properties. In general, for members subject to concentric axial force (tension/compression), the rigidity can be expressed as L/EA, and the flexibility is reverse of the rigidity, EA/L. For flexural (bending) force, the rigidity is L/EI, and the flexibility is EI/L.

Another way to look into the terms of strength and flexibility is by looking at its stress-strain curve. By definition, strength of a given material is the capacity of an object made out of it to withstand great force or pressure, F = \delta x A. Therefore, in the diagram below, the strength goes up for an object with greater pressure/stress capability. The vertical line provides an interesting insight - the stronger object needs more force to produce an equal amount of strain (change in length/original length) as the weaker objects.

On the other hand, the flexibility can be defined as how easy an object able to change, which can be thought as strain (rate of change in length) in the diagram below - the higher the strain, the more flexible the object. Interestingly, the horizontal line tells that at a constant stress, the stronger object is less flexible than the weaker objects. Sometimes, it leads to the realization that stronger object/material has higher tendency to fail in a brittle manner.

Now we are ready to introduce the young's modulus. By definition, it is the stress over strain in the elastic (linear) range. Mathematically it is the slope of the straight portion of a stress-strain curve, E = stress/strain = raise (strength)/run (flexibility). I'll stop here, and let you to work out the remaining. Hope I didn't confuse the issue and mislead you.