2

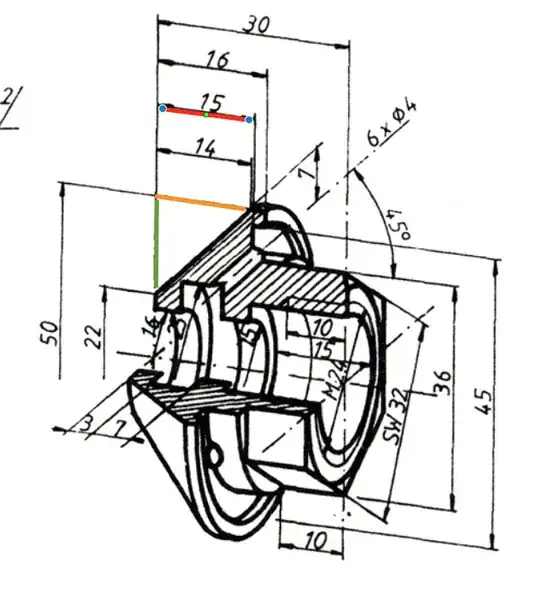
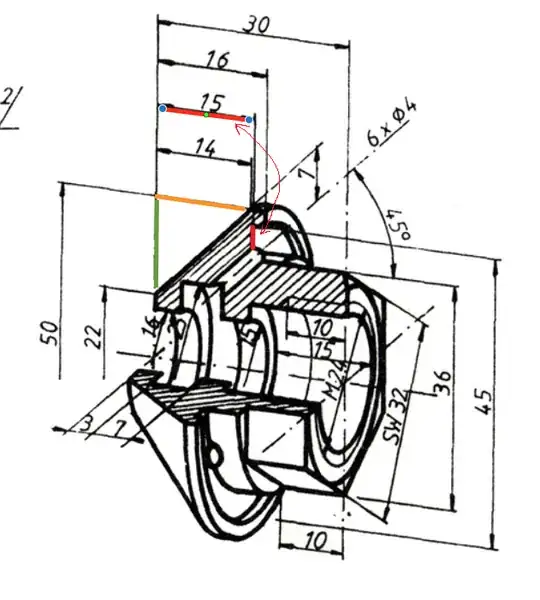
I'm trying to find out the angle/ length of the oblique line, or the solid angle of the conic part.

This is what I've tried so far: According to the pythagorus theorem the length of the line is equal to: $$\sqrt{(50-22)^2+14^2}$$ but obviously this method gives a contradictory results, because as you can read, the line makes a 45° angle with the vertical axis, so its length should be equal to: $$\sqrt{14^2+14^2}$$

I make somewhere a mistake which I obviously don't see it.

The next question is about the dimension 15 ( marked in red ). I spend an awful amount of time to figure it out, but still cannot say anything.

At the end I want to know if this is something I'll confront a lot in real life mechanical engineering ? I mean a really confusing old drawings of parts sometimes with wrong/incomplete dimensions ? enter image description here

Amazon Dies In Darkness
  • 111
  • 1
  • 1
  • 5
Sam B
  • 334
  • 1
  • 2
  • 10

1 Answers1

6

50 and 22 refer to diameters of the conical bit. Usually in axisymmetric objects you denote diameters. It is the same as the 36 and 45 diameters (which are more easily understood).

So it is:

$$\sqrt{\left(\frac{50-22}{2}\right)^2 +14^2}$$ $$\sqrt{\left(14\right)^2 +14^2}$$

So there is no contradiction.

Regarding the 15, it actually refers to the distance of the highlighted small channel at the underside of the conical bit.

enter image description here

NMech
  • 24,340
  • 3
  • 38
  • 77