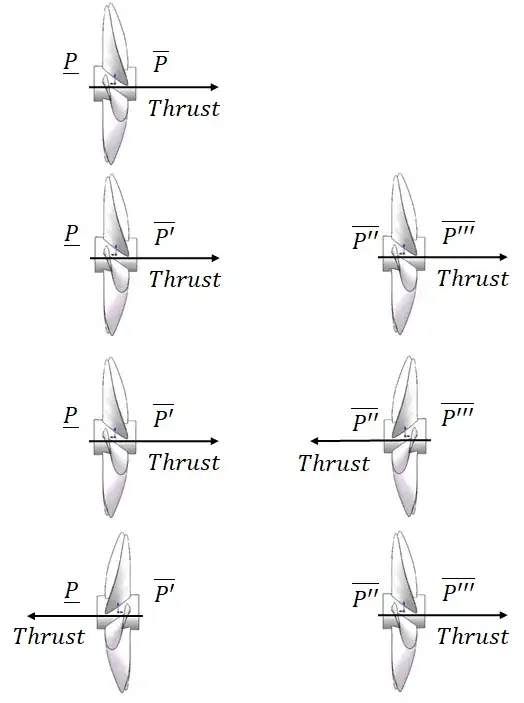
- All propellers shown in the figure above are identical and are operated at identical speeds with four separate (numbered 1 through 4 vertically) configurations illustrated. The physical distance between the cross sections of any two propellers is small and is close to the diameter of a propeller.
- Each configuration is open to the air (for instance mounted on a common axis in the lab) and not enclosed within a pipe or a container.
- In the top figure, $\bar{P}<\underline{P}$, with similar air pressure relationships for all the propellers shown in the rest of the figures which correspond to the directions of thrust obtained from each propeller shown in the figure. Using Bernoulli's equation we can state the relationship $\underline{v}<\bar{v}$ between the speeds corresponding to $\bar{P}$ and $\underline{P}$.
- Using Bernoulli's principle or other intuitive fluid flow concepts, we would like to understand the relative efficiency of the configurations, where the metric of efficiency is the ratio of the sum of the magnitudes of the thrusts of both propellers (in any of the configurations 2 through 4) to twice the thrust of the propeller in configuration 1.
We're mostly concerned with the comparison of the second, third and fourth configurations. Using Bernoulli's equation, the second configuration seems to be non-degrading if not beneficial to the performance (sum of individual thrusts) while the third and fourth are difficult to analyze by this approach since the flow reverses in the region between the two propellers. If we look at the speed of the air flow (air is thrown with high speed on the propeller side opposite to the direction of thrust), the propellers in configuration four affect each other's performance the most perversely. However, it is difficult to assess the comparison of the second and third configurations. The propellers are co-axial although powered by distinct motors and are open to the air. We can assume still air at atmospheric pressure and density with zero ambient flow rate for the purposes of the question. The back-pressure between the propellers is the object of analysis since knowing it would mean we know (at least a part of) the thrust magnitudes.
Which configurations will generate the maximum sum of the individual thrusts? Can we explain the reasoning intuitively (using Bernoulli's equation or other fluid flow concepts) for the higher efficiency obtained in some of the configurations?