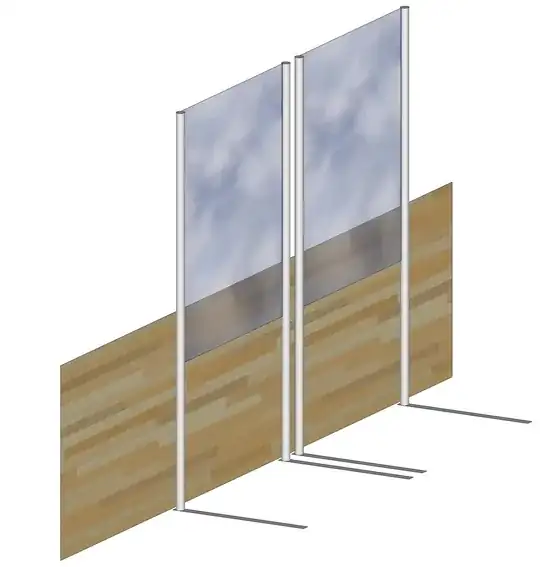
This is a side view of the panels
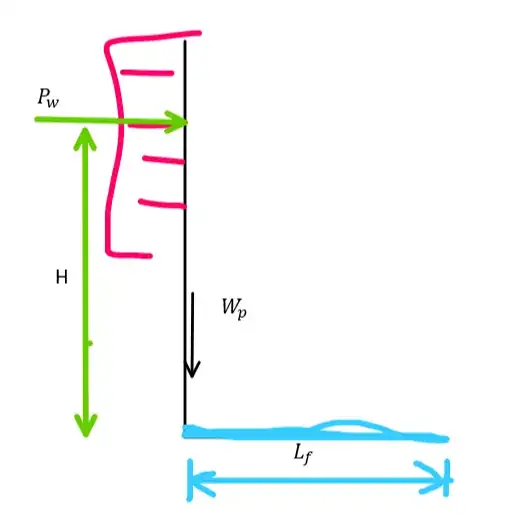
where:
$H$ is the height of the resultant concentrated wind force $P_W$ from the ground. Given the parameters of the problem, H should be equal to :
$$ H= \frac{1+2.75}{2}= 1.875 [m]$$
$L_f$ is the total length of the horizontal part of the feet. The length of the feet will affect the weight, and the total weight of the feet $W_f$ will be equal to :
$$W_f = 2 L_F \cdot q\cdot g$$
where:
q is the mass per meter (1 kg/m)
g is the acceleration of gravity (~10 $m/s^2$)
2 is because there are two (2) feet per stand
therefore:
$$W_f = 20 \frac{N}{m} L_f $$
$W_p$: is the weight of the vertical part of the panel (glass and metallic part). I will be assuming here that the weight is about 10 kg (i.e. 100 N).
$P_W$ is the total force of each panel (assuming that there is a uniform pressure on the panel (this is a semi valid assumption, but its simple enough to present here). This is the most involved part so I will break it up.
wind panel
In order to calculate the wind force on the panel:
The nominal wind pressure is $q_p$
$$q_n = \frac{1}{2} \rho v^2$$
where:
- $\rho = 1.225[kg/m^3]$ is the air density
- $v$ is the air velocity (6[m/s])
The wind pressure $q_p $ on the flat panel is
$$q_p = C_d \cdot q_n = C_d \cdot \frac{1}{2} \rho v^2$$
where:
- $C_d$: is the drag coefficient.
The total wind force $P_w$ on the panel is:
$$P_w= q_p \cdot A = A\cdot C_d \cdot \frac{1}{2} \rho v^2$$
Moment equilibrium.
If the wind blows in the direction of the initial image, then the panel will start to rotate/pivot around the rightmost part of the feet in the image (lets call that point A). In that case the moment equilibrium about A, will be:
$$\sum M_A = -P_w H + W_p \cdot L_f + P_f\cdot \frac{L_f}{2}$$
This need to be positive in order for the panel not to rotate about A. Therefore
$$\sum M_A \ge 0 \Rightarrow -P_w H + W_p \cdot L_f + P_f\cdot \frac{L_f}{2} \ge 0 $$
I will substitute the parameters that are depended on $L_f$:
$$-P_w H + W_p \cdot L_f + 20 \frac{N}{m} L_f \cdot \frac{L_f}{2} \ge 0 $$
$$ \frac{20 \frac{N}{m}}{2}L_f^2 + W_p \cdot L_f - P_w H \ge 0$$
You can then solve this equation and obtain two solutions. One will be positive and one will be negative. Values greater than the positive value, and values smaller than the negative value will satisfy the above requirement. (The negative value makes sense, because negative $L_f$, just means that the feet extend to the left).
Note that you should investigate also the other way overturning (wind blowing from the right.
another solution instead of really long feet.
Provided the existing fence has adequate structural capacity, you could try the following solution.
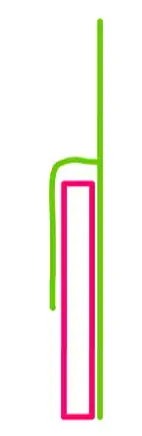
where:
- red is the old fence
- green are the new panels.