Hydrostatic forces

Question

Hello I had a quick question regarding this homework problem. The tank in the figure is 120 cm long into the paper. Determine the horizontal and vertical hydrostatic forces on the quarter-circle panel AB. The fluid is water at 20 C. Neglect atmospheric pressure.

To find the horizontal forces I think it its quite straight forward however, I am having difficulties finding the vertical forces, would anyone be able to direct me in the right direction? How do we find the vertical force of this AB panel if there is no water on top, do we just pretend there is water above this AB panel?

Answer 1

There are two approaches to solve this question.

Approach 1- Vertical force acting on panel AB is equal to weight of fluid column above the panel and since there is no fluid above the panel here so in order to find out the vertical force on the panel we assume that fluid is present above the panel (consider upto free surface) and the magnitude of vertical force is equal to the weight of the fluid above the panel upto the free surface and it’s point of application passes through centre of gravity of that imaginary fluid column.

Approach 2- Consider the fluid element (as shown in figure) and do force analysis, so for equilibrium of fluid element net force must be zero. So from there you can calculate vertical force.

From both approaches you will get same answer.

Answer 2

Hydrostatic pressure is equall in all directions horizontal and vertical or any other direction. and if as you say we ignore the atmospheric pressure,

$$ P=\rho g h$$

• $\rho = density$

• h = depth

So as long as the round panel in blue is connected at bothe ends to the rest of the container its hydrostatic pressure at any level is only depending on its dept, not the direction.

Answer 3

Let's review the statements from the elementary fluid mechanics:

$p = \rho gh = \gamma_wh$, where $\gamma_w = \rho g$ is the specific weight of the water. Because no shear stress exists in a static fluid, all hydrostatic forces on any element of a submerged surface must act in a direction normal to the surface.

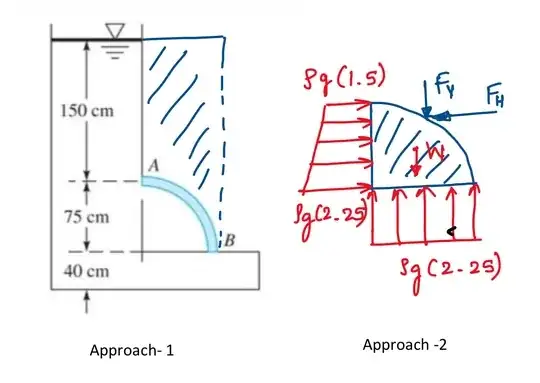
Now let's see your question. Since the water above point "A" exerts a constant pressure at that elevation, and the water below point "B" has no effect on the curved panel, for simplicity, we can hide them and only focus on the body of water that directly exerting pressure on the panel.

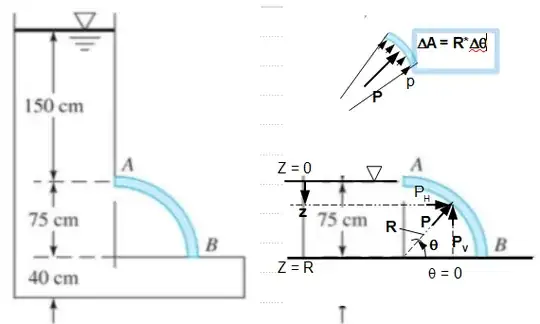
From the figure on the right, you can write the equation for the equations:

$p = \gamma_w*z$

$P = \gamma_w*z*\Delta A$

$P_V = \gamma_w*z*\Delta A*Rsin\theta$

Now you can write the equation in derivative form and take double integration ($z, \theta$) to get Pv, which shall be acted through the centroid of the area under the curve.

Before finishing the calculation, don't forget to add the pressure due to the water above plane a-a though.

Note the presentation is the concept, you need to do the math. And please check the equations which may contain mistakes. (You can verify the equation by checking the $F_H, which is known for sure.)