Calibrating a system with matrices

Question

I have several monochromatic LEDs that are coupled with controlers (PWM), thermometers and light sensors (spectrometer).

For each LED:

• The controlers allow me to change the voltage/current applied to the LEDs, which, in turn, modulate the light's intensity (I call the value Input)
• The thermometers measure the Temperature of the source
• The spectrometer measures the actual light intensity at several wavelengths (typically 101 points between 400 and 700 nanometers), it measures the 'Spectral power distribution' (SPD) of the LED.

My objective is to build a robust representation of the LED behavior. I need this because I observed that the SPD variation is non-linear: it varies with the Input but also with Temperature, and the greater the Input the greater the Temperature. The heatsink is an active cooling system so I can modulate the temperature and see the result in terms of Output

What typically happens is that the LED color (and SPD) will change when the Temperature changes: for the same Input, if the Temperature is low, the LED will have a greater overall Output and its peak emission wavelength will be shorter (say 590 nanometers). When Temperature rises the overall Output will be smaller and the peak wavelength will be longer (for example 605 nanometers).

In practice, this means that a yellow LED will behave like a Red LED at higher temperatures. If I have a robust representation of this behavior, I can get a better prediction of my LED 'Output' and adjust my cooling system to get the color that I want.

_

For simplicity, I have restrained my analysis of the SPD to only one wavelength in the following example. The idea behind this approach is that if I have a model of the system's behavior for each wavelength that depends on the same variables Input and Temperature, I will be able to represent my LED in every possible practical situation:

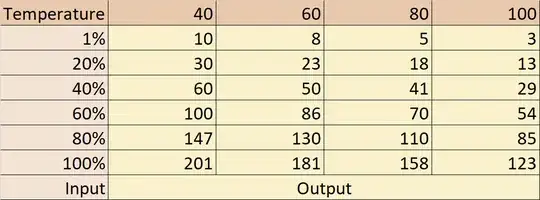
Output corresponds to the value of one of the 101 channels of the spectrometer, 'Temperature' is an indicator of the LED temperature measured on the heatsink, 'Input' is the PWM control value applied to the LED, that varies between 1% and 100%.

There is a quite clear relationship between the 3 variables and I am searching for a function:

Output(Input, Temperature)

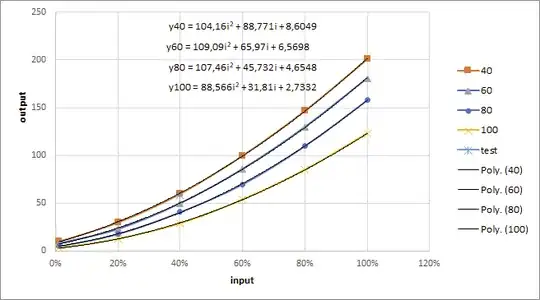
It seems quite clear that a 2nd degree polynomial function fits well with the relationship between Input and Output at a given Temperature:

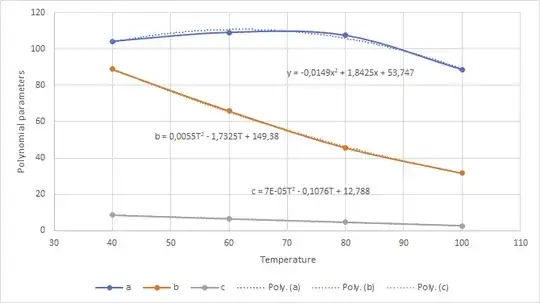
And another 2nd degree polynomial can fit the varying parameters of the first function, in relation to Temperature:

How would you proceed to build a representation of such a system? Since I have hundreds of such Output datapoints associated with Wavelength, Input and Temperature, I thought that it would be useful to use matrices to represent the system with non-linear polynomials?

Answer 1

It seems that you have two independent control parameters, the input and the temperature. You have a choice on where you decide to set the dependencies. Suppose we define $I$ for input, $T$ for temperature, and $O$ for output. You might decide to make each term in your polynomial a function of temperature.

$$O = A(T)I^2 + B(T)I + C(T)$$

Alternatively, you might decide to represent the functional form as a separation of variables.

$$O = \left(AI^2 + BI + C\right)f(T)$$

When you have a first principles reason to choose one or the other equation, do so. Alternatively, you may want/need only to do an engineering empirical approach. The simplest expression to handle is the separation of variables with $f(T) = T$ (temperature is a linear multiplier over all other parameters). Your plots show that this approach will likely not work robustly. The second plot suggests that the first two terms are non-linear and the third term (constant $C$) is linear in temperature.

$$A(T) = a_1T^2 + a_2T + a_3$$ $$B(T) = b_1T^2 + b_2T + b_3$$ $$C(T) = c_2T + c_3$$

The full analytical expression that combines all expressions above is not amenable to an easy analysis, especially also when it is to be done over hundreds of values. The full analytical expression is also not easily amenable to a linear algebra decomposition (if at all). The approach that you show to obtain quadratic analytical expressions using just a small subset table is a reasonable start.

The next step would do non-linear regression fitting to an entire set of data using the combined functions. The objective would be to obtain fitting constants and their regression uncertainties, for example $a_1 \pm \Delta a_1$, $b_1 \pm \Delta b_1$, $\ldots$. This is an advanced level of work that is not within the domain of typical spreadsheet applications. Search for software to perform multi-parameter non-linear regression fitting to review options.

Finally, when you have the non-linear regression values, you can apply them in the linear propagation expression for relative uncertainty in output $\left(\Delta O/O\right)^2$ following from the basic theme previously mentioned (although such an approach may be exhaustive).