Parallel beam load cells, force transfer and maximum load

Question

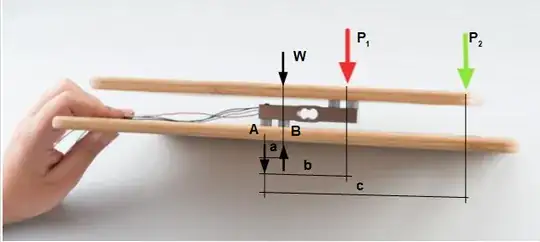
I'm going to experiment with a parallel beam load cell like this one: https://cdn.sparkfun.com/datasheets/Sensors/ForceFlex/TAL220M4M5Update.pdf. I've read somewhere that for a setup shown on this picture:

the response of the cell is largely independent of the place the force is applied to the top plate, e.g. a mass placed in the spot indicated by red or green arrow, they will produce the same load sensor response. Is that accurate?

In my use case, the force will be applied where the green arrow points. I want to make sure that I'm not exceeding the safe overload for my sensor.

EDIT

The gist of my question is whether the sensor response will be proportional to force times distance from the center of the cell (moment of force) or there is some other formula.

EDIT'

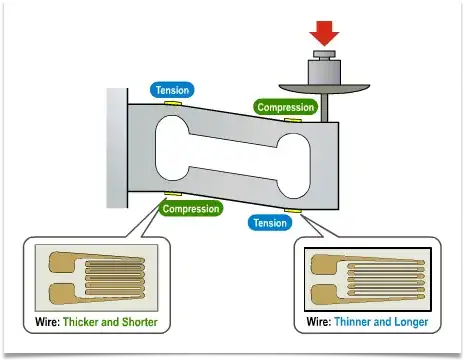
Here is the drawing showing compression and tension directly measured by bending beam load cell:

BTW, I'm not interested in highly accurate measurement, just an approximate detection of an object with a mass above a certain threshold.

Answer 1

The datasheet of the TAL220 mentions parallel beam type. This is (probably) the same as what is more commonly know as double bending beam (however the shape can also also allude to shear load cell). In any case all those types are fairly insensitive to the application load.

If I were in your shoes (i.e. I was stuck with a product), and if you are certain that the point of load remains constant (changes less than 10%) all I would do is calibrate the signal. I.e. put different loads on, see the response, and interpolate.

E.g. I would put a weight at the threshold (e.g. 3kg) and see the values at the closest, furthest and most likely position. If you got 3.5,3.8, and 3.6 respectively, and you are ok with a $\pm$0.5 kg error, then I would just set the 3.6 as a threshold.

(Although, I expect that the above procedure would give you acceptable results,) in the event that the desired accuracy is not achieved, I would try to redesign the platform to bring the load application closer.

Answer 2

Correct. The position of forces will affect the reactions at points A & B as shown.

$\sum M_A = 0$

$R_B = \dfrac{W*a + P_1*b + P_2*c}{a}$ (Compression)

$R_A = W + P_1 + P_2 - R_B$ (Tension)

Note: W = Weight of the top plate (conveniently assumed its centroid falls on point B). The weight of the lower lever arm is ignored in the calculation.