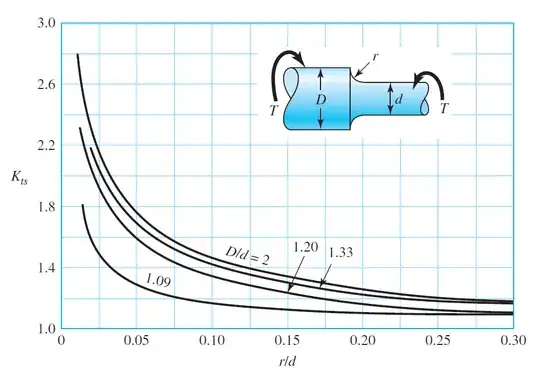
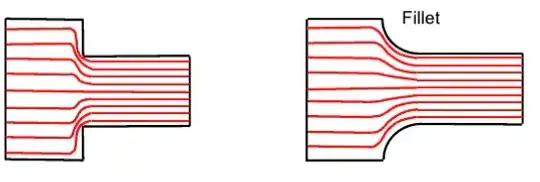
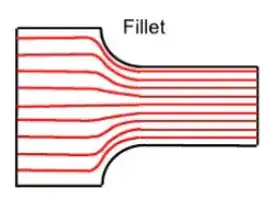
I have seen plenty of diagrams showing parallel axial stress lines to aid in understanding the stress concentration around corners and other things. But this doesn't seem to be a good visualization for shear stress concentration.
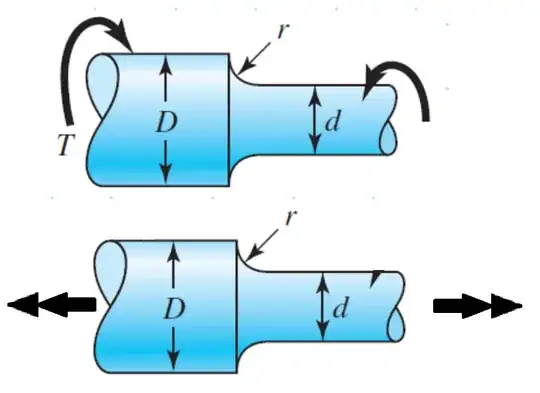
For example, in the below diagram, there is shear stress concentration around the fillet. But in my head, I visualize the part's parallel planes being twisted against each other, with the "lines" not crossing between the planes. In that case, how am I able to visualize the shear stress concentration occurring here? I am having trouble understanding the concept since I can't picture (a model of) what's really going on.