Does perfectly elastic and perfectly plastic material make any sense?

Question

I have been reading about the elasticity of materials and most often in engineering there is always some ideal concepts which are the extreme cases. So is there any particular definition to what is a perfectly elastic and perfectly plastic material?

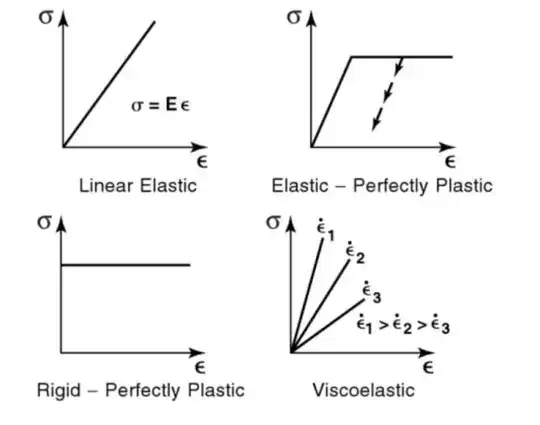
Perfectly Elastic Material

A lot of people say that from material science point of view a more elastic material means the material has greater resistance to elastic deformation eg steel being more elastic than rubber . With that definition ,a perfectly elastic material should then be defined as " a material which suffers zero deformation under any value stress (within elastic limit)". But in this case it becomes similar to the definition of a rigid body , which is "a body that suffers no deformation under stress".

Yet another possible definition could be that a perfectly elastic material is one which behaves as an elastic material over its entire stress-strain curve i.e behaves as an elastic material till fracture. Here then we could have perfectly linear elastic material and perfectly non-linear elastic material.

Perfectly Plastic Material

A perfectly plastic body could be defined as one which produces no restoring force for any value of stress applied. Thus a perfectly plastic body would always suffer permanent deformation for any value of load applied or in other words a perfectly plastic body would show plastic behaviour throughout the stress-strain curve.

If perfectly plastic and perfectly elastic are well defined ,how would their stress-strain curve look like?

Answer 1

If I understood correctly you are only after the stress-strain curves.

Figure: Stress strain curves for different types of materials (source What's pipping)

• Perfectly Elastic : (referred to as Linear Elastic) returns to its original shape, and the force is proportional to the deformation (definition may vary)
• Perfectly plastic : (referred to in the image as Rigid Perfecly Plastic): A material that does not produce a restoring force after deformation.

Additionally, two other types of materials are presented:

• The Elastic-Perfectly Plastic which is a common simplification for materials that deform up to a point elastically, then deform plastically, and only partially return to the .
• the Visco-elastic where the force is depended on the strain rate.

The problem is that in most cases these models, don't necessarily represent a real material, so there is an confusion in the literature depending what you are looking at.

Usually the elastic refers to either:

• the relationship between the proportional relationship between stress and strain
• the ability of the material to return to its original form/position

Usually the plastic refers to a material that retains all or some of the deformation.

Answer 2

This is not to answer your questions but the comment on the modulus of a material in the plastic range, which I consider is undefined rather than zero because both the stress and its increment are non-zero.

The upper graph is the stress-strain curve of rubber. The lower graph is the stress-strain curve of silicon rubber. (Note the line between the two points of interest is idealized as straight)

ADD: I suggest reviewing the practice and reasoning of using the "Offset Method" to determine the "yield point" for some ductile materials. (While it differs, as it is well defined, from the case I've shown, which is not defined and accepted by the engineering community, the concept is similar - a modulus relating stress and strain can be defined in any region along the curve if needed, and it wouldn't be "zero" unless the increment of the stress is zero or negative.)

Offset Yield Method

ADD: Unrelated to my writeup here, but provided for your information - "Perfect plasticity is a property of materials to undergo irreversible deformation without any increase in stresses or loads."

Answer 3

I believe the answer to this question depends on what kind of perspective you use. I won’t get into details on the two materials type as they have already been well described in other replies. I will focus on what is my point of view on this:

• from an engineering standpoint I believe the two materials make sense. In the way that stress applied to the material are well within its elastic region thus it behaves as a perfect elastic material. Imagine bending a steel H beam with few Newton, the response is basically perfect elasticity. In a simile way if you load it with multiple tons then you will be analyzing something good similar to perfect plasticity

• from a material science point of view then I think it makes less sense if not for modeling purposes

Answer 4

A perfectly elastic material is simply one that always returns to original shape after loading.

A perfectly plastic material is one that always plastically (permanently) deforms under load.

The shapes of the stress-strain curves can practically be whatever, as long as the material follows the "rules" above, then it will be considered those things.

These terms are used as estimations and for mathematical modeling and categorizations. There isn't truly any material that is either. All materials will behave between the two extremes at different points, more or less. But quartz is typically considered the most perfectly elastic material, and wax or putty is close to perfectly plastic. These materials have their own values for their engineering properties (quartz is very stiff, putty is soft), but a material that is either perfectly elastic or perfectly plastic does not have to have those same values. They could have any slope values eminating out from around the origin (0,0). It's just "difficult to make" a material in specific ways because physics/nature is just the way it is.

Most materials but not all (that we consider in engineering) are generally "elastic perfectly-plastic", meaning they have an elastic region and what can be estimated as a perfectly-plastic region. That being said, a stress-strain curve does not presuppose an elastic region-- the elastic region is marked/noted on the curve IF and only IF elastic behavior is observed. That is to say, you can (theoretically, hypothetically) have a curve that LOOKS like it has a typical elastic region, but indeed it does not return to it's initial shape after load is released. And as someone else mentioned, not all elastic regions are linear.

I believe something like cast-iron or graphite could be considered (fairly) perfectly elastic since it doesn't really have a plastic region to speak of. These are "brittle" materials, and their yield and ultimate tensile strengths are considered equal. So, their whole behavior (up until break) is "perfectly elastic".

And, just for completeness, a rigid body is one that doesn't deform (either elastically or in a plastic way) under load-- or, for estimation/relative purposes, deforms very little under load. A rigid body doesn't have to be elastic or plastic to be considered rigid (but, of course, it could be one or the other).