1

I'm presented with a problem requiring some analysis to determine if an antenna bracket mounted to a concrete blockwork wall is sufficiently strong enough to endure a wind load given the known surface area of two antennas mounted on it.

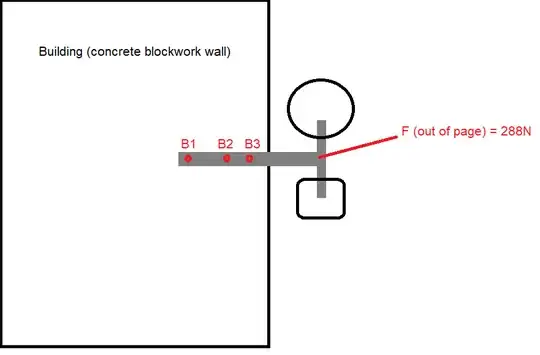
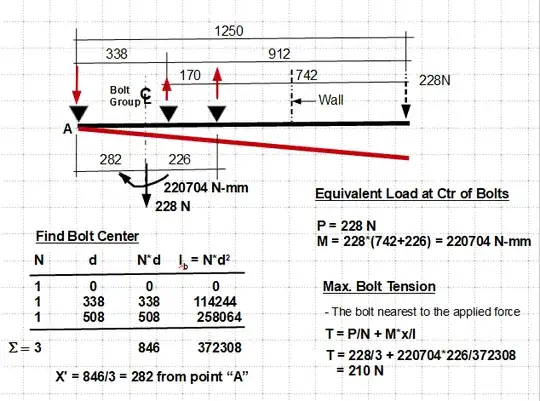
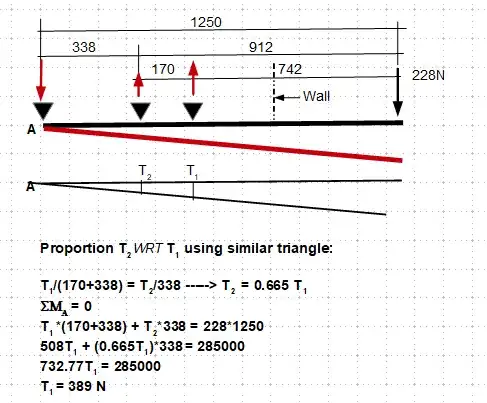
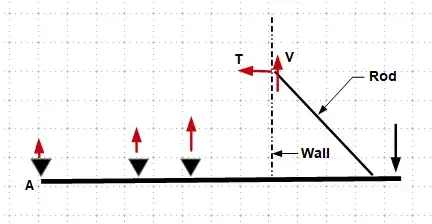
Excuse the terrible diagram: enter image description here

The force due to the surface area of the antennas & wind velocity is assumed to be 288N at the end of the vertical post acting out of the page and attempting to 'lever' bolts B1:B3 out of the wall (pullout/tensile force).

Distance B1 to force = 1250mm, B2 to force = 912mm, B3 to force = 742mm

I've simplified the problem to assume B2 doesn't exist, B1 is the fulcrum and B3 is the 'load' in a class 2 lever system: enter image description here

For the simplified system I work out the tensile force acting on B3 to be in the realm of 709N:

(1250/(1250-742))*288N = 708.67N

Having an electrical background I'd be very interested to hear how a mechanical engineer would approach the problem and whether there is a better way (than my simplified system) to represent the forces on each of the 3x bolts.

TMcC
  • 13
  • 3

3 Answers3

1

Assuming the lever is rigid enough not to bend to simlify our estimate:

The lever will rotate about B1 bolt because it can not penetrate the concrete block. So B2 to and B3 will share the 288N proprtionaly to their distance from B1. Lets call their reactio RB2 and RB3 respectively.

$$R_{B3} =(1250-742=508)/(1250-912=338)*R_{B2}= 1.5 R_{B2}$$

By substituting tension in B3 as 1.5 B2 we get

$$ \Sigma M_{B1}= 0, \ R_{B2}*338mm+ 1.5 R_{B2}*508mm= 288N*1250 \ \rightarrow \\ R_{B2}=327N \ R_{B3} =327*1.5 = 490N $$

kamran
  • 23,517
  • 2
  • 22
  • 42
1

For small equipment mounting, let me introduce two simple methods:

1) Rigid Rotation Method (Classic)

enter image description here

2) Cantilever Method (Conservative approximation)

  • Assume cantilever action, for which the applied load rotates about the point "A", and the rotation is restricted by the two bolts farthest from the point "A".

enter image description here

Conclusion:

I recommend using the Metod 2 for its simplicity and embed safety. Also, I suggest adding a rod from the fixture to the wall to take care of the vibration induced by wind.

enter image description here

Please check my math for mistakes.

r13
  • 8,333
  • 3
  • 10
  • 29
0

As mentioned in kamran's answer its very important that the bar is rigid. Otherwise the following analysis is not relevant.

Although you don't seem to consider it this way, -if the beam is rigid enough-, then the fulcrum at the far left edge of the beam (not on B1, so the force there is not zero). The equation I derived is based on that assumption, which is more correct and will give slightly different results (the accuracy will depend on the beam's rigidity).

Below is an image of the side and top view of the beam (bracket to my mind has a right angle somewhere)

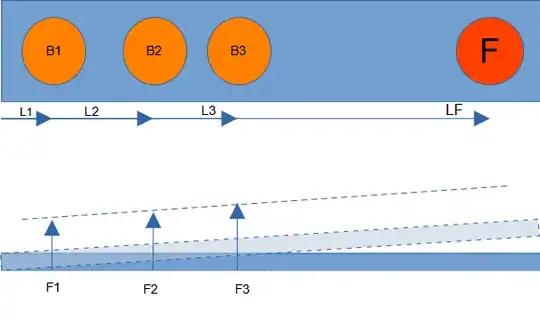
enter image description here

The top view (its at the bottom - I'm using a first angle projection), shows

  • the undeformed with solid lines and
  • the deformed position with light blue and dashed lines.

From there you can see that the displacement for each bolt, is going to be proportional to the distance of the bolt from the fulcrum. The fulcrum is the far left of the beam. Because the force is proportional to the displacement then the force on each bolt will be equal to:

$$F_i = K\cdot L_i$$ where:

  • $F_i$ is the force on each bolt
  • $K$ is the spring coefficient of the bolt (which eventually you need to calculate)
  • $L_i$ is the distance of the bolt from the fulcrum .

Then you can write the equations for the equilibrium of moments about the fulcrum :

$$ F_1\cdot L_1 + F_2\cdot L_2+ F_3\cdot L_3 - F\cdot L_F =0$$ or $$ \left(K L_1\right)\cdot L_1 + \left(K L_2\right)\cdot L_2+ \left(K L_3\right)\cdot L_3 - F\cdot L_F =0$$ if you simplify that: $$ K \left(L_1^2 + L_2^2 + L_3^2\right)=F\cdot L_F $$ therefore: $$ K =F\cdot \frac{L_F}{\left(L_1^2 + L_2^2 + L_3^2\right)} = \frac{L_F}{\sum_{i=1}^{3}L_i^2} \cdot F$$

Now that you have K, you can calculate : $$F_i=K \cdot L_i$$

numerical example

This is to illustrate the difference, of selecting a different position to the fulcrum point.

if you assume the fulcrum is at B1, then you end up with (essentially the same with kamran's computation)

$$F_1=0 N, \qquad F_2= 326.86 N , \qquad F_3= 491 N $$

if you assume that the fulcrum is 100 mm to the left then the above values become $$F_1=68 N, \qquad F_2= 297 N , \qquad F_3= 413 N $$

NMech
  • 24,340
  • 3
  • 38
  • 77