1

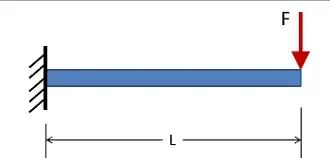
I am not a mech engineer and have been struggling with this for a while, I feel like it is pretty straight forward but I'm missing something.

The problem is a horizontal tube that is supported at one end with the weight on the other end. My specs are length of 3 ft, outer diameter of around 2 inches, and a force of 120 lbs.

A diagram: enter image description here

Basically I want to figure out the optimal outer diameter (2 inches +- .5 inches or so) and minimal wall thickness. (The cheapest tube)

I can get tensile strength from most carbon fiber tube manufacturers.

I believe I want to calculate maximum stress and more specifically sheer stress for a hollow tube. But I haven't been able to find the calculations that are in terms of tensile strength.

Any pointers or references in the right direction would be awesome!

Joshua von Damm
  • 11
  • 1
  • 3
  • The short answer is you can't. The mfg. might have the info. It depends on the very fine details of the fiber orientation within the tube. Tiny variations in manufacturing can have a huge impact. Carbon laminates are horribly non-isotropic. The failure mode here will be buckling, with the stress profile varying along the tube. Finding the buckling mode, and point of buckling, for a non-istropic tube in bending and shear, is not for the faint of heart. – Phil Sweet Jun 02 '22 at 09:55
  • Unless you can afford exhaustive testing, you'd be better off with a material that is more isotropic, and can be designed with a wall thick enough to simplify the buckling analysis. Aluminum would be my choice. Sans a testing program, aluminum would probably be lighter for most L/D ratios of interest. – Phil Sweet Jun 02 '22 at 09:56
  • Why do you not use metric units? – 12431234123412341234123 Jan 23 '24 at 12:39

1 Answers1

0

if we assume the tube carbon fiber has equal tensile and compressive strength and young modulus, which is not necessarily true in all cases. and with a negligible mass.

Then we have $$ M= PL = 120*3*12=4320lbs.inch$$

$$\sigma =M/S \quad S= \text{section mudulus}= 4320/s \quad , \ S=\sigma/4320$$ and for a hollow tube beam

$$S= \frac{\pi(d_2^4-d_1^4)}{32d_2}$$ And having $\sigma$ acceptable stress of your material you can find the thickness $d_2-d_1$

Shear stress is $$V=12*1.5 / A_{beam}= 180lbs/(\pi(r^2_2-r_1^2))$$

These are low stresses and most likely any size commercially available will do the job.

But if your carbon fiber has different E, young modulus for tension and compression and different strength then you have to find the neutral axis which will shift up or down from the geometric CG by the ratio E1/E2, E= young modulus, and find the S and take it from there.

kamran
  • 23,517
  • 2
  • 22
  • 42