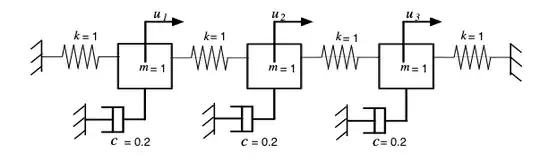
The Problem
I have the following system for which I would like to determine its dynamic response, taken from these lecture notes pg.20:
where the forcing functions are $u_1 = 1-U(t - t_0)$, $u_2=0$, and $u_3=0$, $U(\cdot)$ is the unit step function and $t_0 = 2\pi/\omega_1$ where $\omega_1$ is the first undamped natural frequency.
My Attempt
I know the time domain representation of the system to be of the typical format as shown in Eq.(1), and therefore the Fourier transform is as shown in Eq.(2):
\begin{gather} \mathbf{M}\ddot{\mathbf{x}} + \mathbf{C}\dot{\mathbf{x}} + \mathbf{Kx} = \mathbf{u}(t) \tag{1} \\ % \Rightarrow [-\omega^2\mathbf{M} + i\omega\mathbf{C} + \mathbf{K}]\mathbf{X}(i\omega) = \mathbf{U}(i\omega) \tag{2} \end{gather}
where since we know that $\mathcal{L}\{1 - U(t - t_0)\} = 1 - \frac{\exp{(-st_0})}{s}$, then the Fourier transform of the right hand side of Eq.(2) is:
$$\mathbf{U}(i\omega) = \left[\left(1 - \frac{e^{-i\omega t_0}}{i\omega}\right),\, 0,\, 0,\right]^T$$
As a result, the dynamic response would be:
$$\mathbf{X}(i\omega) = [-\omega^2\mathbf{M} + i\omega\mathbf{C} + \mathbf{K}]^{-1}\mathbf{U}(i\omega) \tag{3}$$
Since the response by which I am comparing my answer is given in generalised modal coordinates $\mathbf{q}$, then the modal transformation of Eq.(3) follows where $\mathbf{V}$ is the eigenvector matrix thus we know that the modal mass, stiffness, damping matrices should be $\bar{\mathbf{M}} = \mathbf{I}$ (i.e. the identity matrix), $\bar{\mathbf{K}} = \mathbf{\Omega}^2$ (i.e. a diagonal marix containing the square of the natural frequencies), and $\bar{\mathbf{C}} = \mathbf{V}^T\mathbf{C}\mathbf{V}$ respectively. So Eq.(3) becomes:
$$\mathbf{q}(i\omega) = \left[-\omega^2\mathbf{I} + i\omega\bar{\mathbf{C}} + \mathbf{\Omega}^2 \right]^{-1}\left[\mathbf{V}^T\mathbf{U}(i\omega)\right] \tag{4}$$
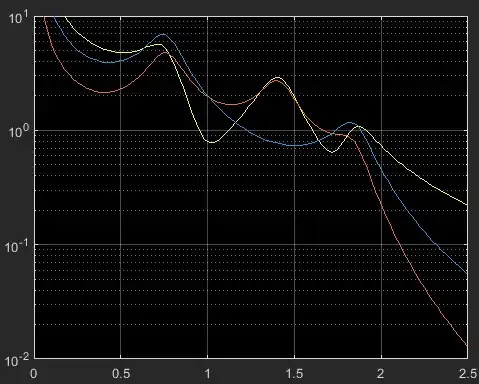
Thefore, the dynamic response would be the magnitude of the imaginary numbers obtained from Eq.(4) above, for all positive $\omega$.
However, when I follow the above steps and solve the problem in MATLAB, the answer is far from the one provided in the excercise. Admitedly, the code is very simple as well (see below) so I struggle to see where I could have gone wrong:
clear ; clc
% Input
n = 3 ; % Number of DOFs
m = 1 ; % Mass [kg]
k = 1 ; % Stiffnes [N/m]
c = 0.2 ; % Viscous damping [Ns/m]
nv = [1 0 0]' ; % Load application vector (load applied to 1st DOF)
% Matrices
M = diag(mones(n, 1)) ;
K = diag(2kones(n,1)) - diag(kones(n-1,1),-1) - diag(kones(n-1,1),1) ;
C = diag(cones(n,1)) ;
% Undamped Natural Frequencies & Modes
[V, Omsq] = eig(K, M) ;
Om = diag(sqrt(abs(Omsq))) ; % Natural Frequencies
% Frequency Aanalysis
t0 = 2*pi/Om(1) ; % Time where unit step is applied
omega = linspace(0, 3, 100) ; % Frequency vector
for i = 1:numel(omega)
s = 1i*omega(i) ;
Us = V'*((1 - exp(-s*t0)/s)*nv) ;
FRF(:,i) = (s^2*eye(n) + s*(V'*C*V) + Omsq)\Us ;
end
% Plotting
figure ; plot(omega, abs(FRF)) ; grid on ; set(gca, 'YScale', 'log') ; ylim([0 10]) ;