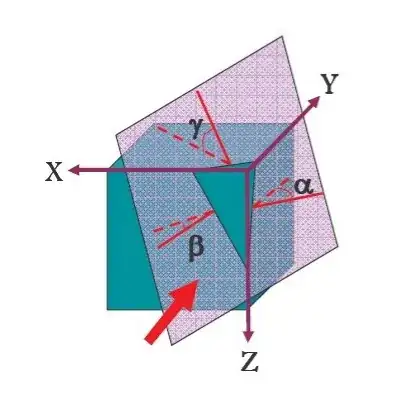
But we know that projection plane is 2D plane where z-component is either zero or constant, so how is it possible projection plane intersects each coordinate axis?
The projection plane is like the film / sensor of a camera. It can be in any orientation, not necessarily parallel to the (global) XY plane. So the projection plane can intersect all three axes except in cases where the plane happens to be parallel to (global) XY or (global) YZ or (global) ZX plane.
I used the qualifier "global" for the axes and the planes since one can define another set of XYZ axes where the X and Y axes lie on the projection plane (horizontal and vertical direction). In that frame, Z axis is by definition, perpendicular to the screen / projection plane.
My question is how to visualize projection from 3D space to projection plane(2D) where diagonal(projection vector) makes equal angle with 3 principal axis ...
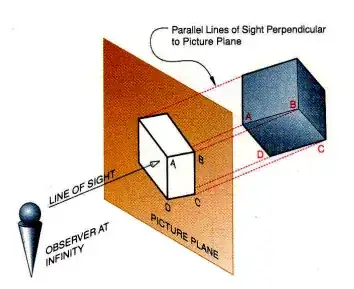
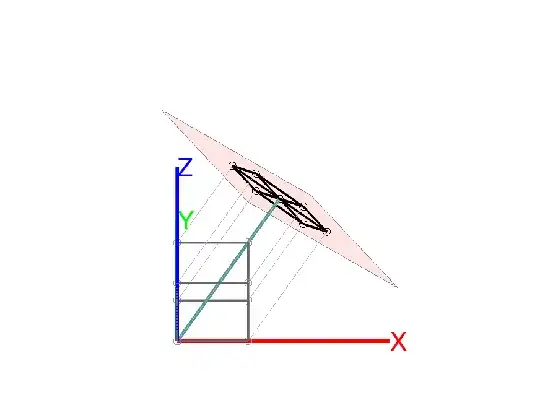
Below are three images which may help you visualize the projection plane, the projection vector / direction and the projected image. The global X, Y ans Z axes are colored red, green and blue. The cube is aligned to the global axes. The projection plane is shown in translucent red square. The projected image of the cube is thick black lines.
The projection direction is shown as thin teal line. Note that all the vertices are extended running parallel to the projection direction until they hit the projection plane.
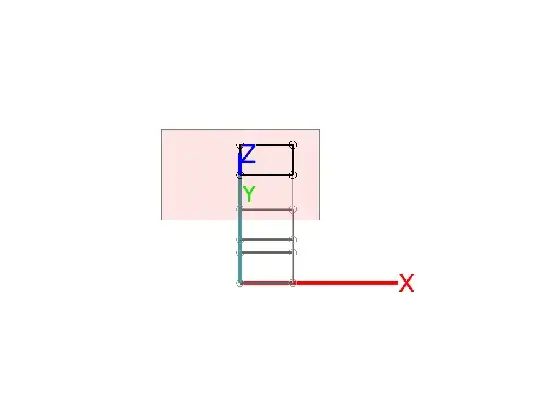
- Projection plane is parallel to the XY plane. The cube appears as a square to when projected on the projection plane.
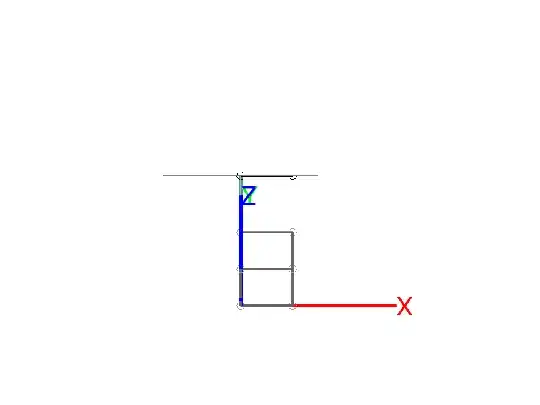
- Projection direction lies 45° to the Z and Y axes. Projection plane intersects Z and Y axes. The cube appears to be two rectangles when projected on to the plane.
- Projection direction is equal angle from all three axes; i.e., projection direction is the vector $[\frac{1}{\sqrt(3)}, \frac{1}{\sqrt(3)}, \frac{1}{\sqrt(3)}]^T$ and the angle with each axis is 54.736°. Projection plane intersects all three axis at equal lengths (not visible in the figure attached). Note that, for this projection, the projection line passes through diagonally opposite corners of the cube.
1.
2.
3.
EDIT
I also read that Projection vector makes equal angles with all of the three principal axes...
Please elaborate how you get $[1/(√3),1/(√3),1/(√3)]^T$
Let the projection vector be a unit vector $\hat{n} = [a, b, c]^T$. The angle that each axis makes with this vector is given by the dot product.
$$
\cos\theta = \hat{x} \cdot \hat{n} = [1,0,0]^T \cdot [a,b,c]^T = a\\
\cos \psi = \hat{y} \cdot \hat{n} = [0,1,0]^T \cdot [a,b,c]^T = b\\
\cos \phi = \hat{z} \cdot \hat{n} = [0,0,1]^T \cdot [a,b,c]^T = c\\
a = b = c \quad \text{since} \quad \theta \triangleq \psi \triangleq \phi
$$
Since $\hat{n}$ is a unit vector, $a^2+b^2+c^2=1^2$.
So, $a = b = c = \frac{1}{\sqrt 3}$.
We can find this vector in another way also;
aligning the projection vector with the cube diagonal
The cube diagonal is $[1, 1, 1]^T$. This vector has length $\sqrt 3$. So the corresponding unit vector is $[\frac{1}{\sqrt 3}, \frac{1}{\sqrt 3}, \frac{1}{\sqrt 3}]^T$