How strong will this sail pull up?

Question

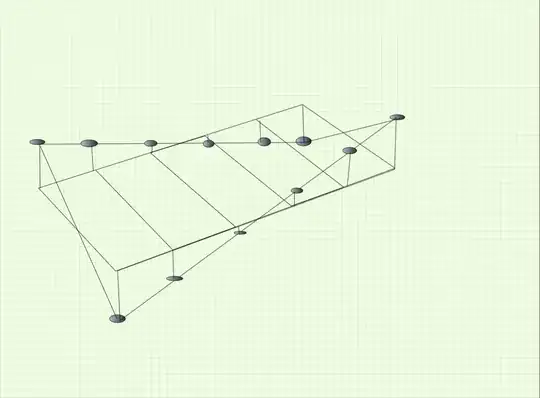
I am building this ground-mounted solar panel sail:

It will sit on twelve 150 mm timber piles. There are 20 panels 1755×1038 mm, 20 kg each, with 17 mm gaps between them, sitting at 69°. The total weight above the timber (panels + aluminium frame) is roughly 550 kg.

The piles are 2.4 m long, and they will be in the ground 1.2–1.5 m deep.

The triangle base is 2.23 m, height 2.91 m and side 3.11 m.

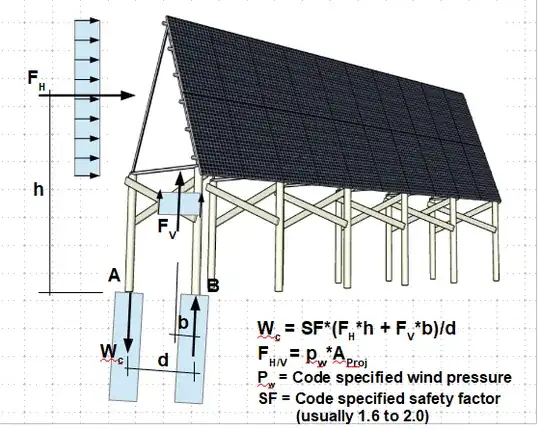
The question is how heavy the piles' feet (not on the picture) need to be to stop the sail from flying away when it storms. The goal is to ensure that a storm would rather rip the structure apart than lift/tip/fly it. Occasionally winds may top 150 km/h in this area.

I've asked a professional structural engineer this question and he's given me this figure of at least 0.6 m³ of concrete per pile.

Assuming density 2.4 t/m³, that means a weight of more than 17 tonnes is required to hold the structure down.

Does the weight figure not sound overestimated? Would a wind be able to come any close to lifting that weight by blowing in the back of this sail before it rips it apart?

Also, will the cross beams between the piles do a good job? My assumption was that they should provide robustness to the structure so that it should not be possible to lift the rear row of piles without lifting the front one to the same distance.

Answer 1

As a rough approximation, the weight of the footing ($Wc$) required to avoid the frame being lifted out of the ground is graphically depicted below.

Answer 2

Unfortunately, the correct answer is not the accepted answer.

Wind code has several load combinations that you need to verify and also pick the scheme that best fits your application and finally calculate the Design Wind Pressure Pw that has a vertical component, Pwv, working on the projected vertical area, Av. And a horizontal component, Pwh, working on the projected horizontal area, Ah.

equating the vertical moments about the end post to zero we get:

$$\Sigma M_v=0 \quad M_{v net}=P_{wv}* Av*1/2\quad \text{length of the sail}-550*1/2 \text{length of the sail}$$

We repeat the above for the horizontal moment:

$$\Sigma M_h=0 \quad M_{h net}= P_{wh}*Ah* \text{free height+1/2 projected sail height}- 550kg*D/2$$

The top line is an overturning moment due to the vertical wind component and to resist it You need a triangular distribution of footings contribution or you can simplify and just divide it by the length of the sail and assume all the moment is resisted by the first and last row of the footings.

The same procedure must be repeated for the horizontal overturning moment. The final result is the sum of the vertical and horizontal overturning moments distributed between the posts according to the geometry of the footings placements. Here is one sketch of the distribution of overturning moments.

'

Edit

After the OP's comment:

To calculate the uplift on each foundation we can again divide uplift forces in two parts: A) uplift due to horizontal wind pressure and B) uplift due to vertical wind pressure.

lets say we arrived at a horizontal overturning moment parallel to the length of the sail as Mh.

Thus it is cancelled by the uplift with a triangular distribution between the 12 footings as follows.

we annotate the pair of footings from left to right as pairs f1, f2.....f6, and the length of the sail, L. and note that 6 posts divide the sail length by 5 parts.

and we annotate the uplift force on the first and last footing as Upf1.

$$ Mh=Upf1 *5/5L/2 + Upf1 * 3/5*L/2+Upf1 *1/5L/2- Upf1*1/5L/2 - Upf1*2/5L/2-Upf1*5L/2 $$

This is a polynomial with one unknown, Upf1, after finding it the other uplifts are proportional to the factors of 3/5, 1/5 and so forth.

The vertical uplift is easier we just divide Mb by D and that the uplift.

depending on the sign we add or subtract them from the horizontal uplift. we need to be careful with signs.

Answer 3

Another thing you need to consider, is the maximum wind pressure that the panels will experience for the calculation -- much depends on this. In the other answers, it's not explicitly mentioned what value should be used.

Solar panels are built to standard specifications. Usually, most solar panels are built to sustain a 200 -300 kg/m^2 Wind load. The actual wind loading value is bound to be in the datasheet. That value should be used (instead of calculated value from nominal airpressure $q_n=\frac{1}{2}\rho v^2$, which is then increased by safety factors).

The reason is that if the calculated air pressure exceeds the specified wind loading then the panel will break off the structure.

Even in the unlikely event that the specified wind loading is less than the total calculated air pressure (this is doubtful because the quoted wind speed of 150 km/hr is quite high -- it corresponds to 41 m/s when Eurocode annexes suggest in the absence of data a maximum average velocity of 25 or in very windy areas 33 m/s), using the maximum value that the panels can sustain is a safer approach.