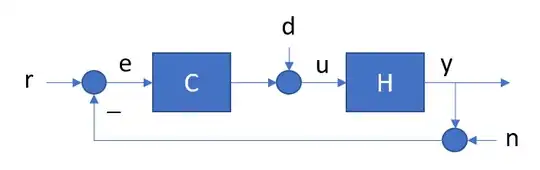
I have a slide here which says following: For the control loop
...apply $d$, measure $u$ and $y$, calculate
$\hat{H}(f) = \frac{S_{yu}(f)}{S_{uu}(f)}$
but then typically
$E\{\hat{H}(f)\} \ne H(f)$
Can someone explain to me the meaning of the last equation? Is it correct to read this line as: "The expected value of $\hat{H}(f)$ is not equal to $H(f)$", and if yes, why is it like this?
In the context depicted in the diagram, the transfer function estimate can be shown to be biased (wrong in expectation) due to the feedback loop. The input will, due to the feedback, be correlated with the noise n that appears in the output, causing the bias.
See, e.g., "System modeling and identification" by Rolf Johansson, chapter 4, for more details.
In fact, several classical identification methods are biased when operating on closed-loop data. This includes several common subspace-based identification methods. Notably, the prediction-error method (PEM) is unbiased also for closed-loop data due to it explicitly taking causality into account (subspace id typically does not).
