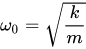Does Bending Stress Affect Natural Frequency?

Question

I have been researching about the factors that affect natural frequencies, particularly about the effects of stresses.

Most of what I have found only discusses compressive and tensile stresses though, that they decrease and increase the natural frequency respectively

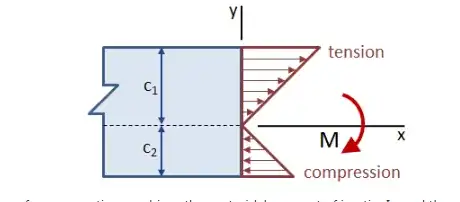
However, I cannot find anything about how bending/flexural stress affects the natural frequency. If I had to assume though, it probably does not affect it, as bending is just a combination of compression and tension occurring at the two sides, and they just cancel out.

Is my guess correct? And if not, can you link additional readings about it. Thank you!

Answer 1

Bending stress is actually the general term to refer to tensile and compressive stresses that develop in a long member by transverse loading, applying a moment to it, or mechanically bending it.

All these lead to the member having tensile stress on the side far from the curvature and compression stress near the inside curve.

Answer 2

The oscillation comes about as the interaction between a position dependent 'restoring force' and an inertia. I put force between brackets as it is a force in a mass-spring system, but can also a torque.

This interaction can be described by the differential equation $m*a = -k*x$ so $m*x"+k*x = 0$ For a linear spring, $x = \sin(\sqrt(k/m)*t)$ is a solution, which is harmonic and with frequency determined by the inertia term 'm' and the spring stiffness term 'k'.

In your bending beam, the 'restoring force' is actually a torque that is the result of the combination of compression on one side of the neutral line and tension on the other side.

Its hard to imagine how to add bending stress without altering either the shape or otherwise the physics of the beam. For strings (under tension) or columns (under compression) this is easily done.

One note (pun somewhat intended): the frequency can change with changing amplitude of oscillation, when the stiffness is not constant. Many materials exhibit spring stiffening. They are thus non-linear springs. This means that the restoring force depends on amplitude (larger deflection, larger-than-proportionally-larger restoring force. Also, the response will not be a simple harmonic anymore.

Answer 3

Frequency is related to force, that is applied and released quickly to produce a forced vibration (oscillation) of an object. The neutral frequency is the property of the material that the object is made of. If the forced frequency is equal to the natural frequency, the vibrations' amplitude increases manyfold. This phenomenon is known as resonance.

In a mass-spring system, with mass m and spring stiffness k, the natural frequency can be calculated as:

Note that the spring stiffness/constant has a unit of "force/length". In it, the length is the displacement caused by the applied force, not stress.