I have two results that don't seem to match up and I can't figure out why.
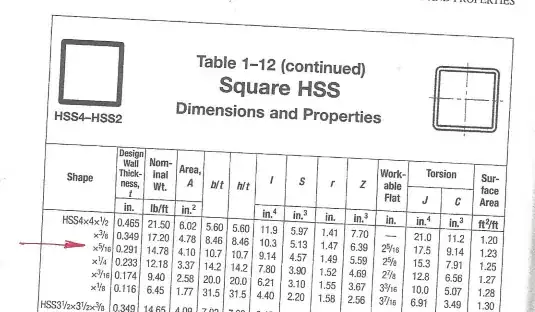
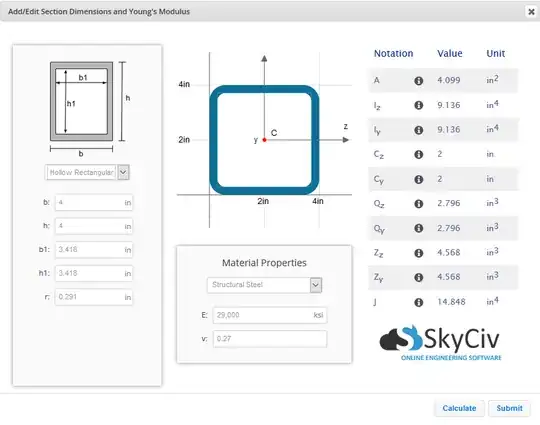
I built a hollow square section (HSS) using two different structural analysis softwares (they both agreed). However, they don't seem to agree with the AISC steel table despite the dimensions being identical. It seems to be the Torsion Constant (J) which is slightly off in the table.
What could be the possible reason for this as I am totally stumped?
Simple formulas for torsion constants of this type of hollow section are all approximate. The AISC tables may be using a different formula from the calculator and making some allowance for the radii at the corners of the section. Or, the AISC values might be derived from a detailed three-dimensional finite element analysis, which will converge to the "correct" torsion constant value.
For "serious" work, use the values from the data sheets, even though for your section the difference is too small to be important.
If you look at the "book" values and the "calculated" value of many shapes, you will often find that there are differences. This doesn't only happen with hollow sections.
The differences are usually small enough that it doesn't matter (and there is as much variation in the material properties).
As @alephzero mentions, most of the variation is from the fillet or radius at the corners.
The fun happens when a given shape changes properties between editions of the manual without changes in the dimensions. Sometimes this is errata, sometimes it is "re-calculating" the table properties to match the "as-rolled" properties. The rolling mill has tolerances, so it may just be that one side of the tolerance is more common than the other. This would skew the average properties.
The approximate equation for the torsional constant, $J$ of a thin-walled square tube is: $$J = tb^3$$ Where t is the wall thickness and b is the width between the wall centerlines.
Using this equation you can verify that SkyCiv is ignoring the corner radius when calculating J.
There's no simple closed-form solution for $J$ with rounded corners, but we can observe that accounting for the corner radii increases $J$. Where the rectilinear corners produced stress concentrations, the curved corners produce a more 'uniform' torsional stress flow, and therefore a torsionally stiffer section. (As least, I think that's a valid mental model.)
You can read the full AISC discussion of torsion in Design Guide 9.
This paper by Darwish and Johnston has a fairly extensive discussion of the effect of corner radii on torsional constants.
