How do heat pumps output more heat kW than the electrical kW used to run the heat pump?

Question

I understand that a 2 kW electric heater will use 2 kW of electricity and output 2 kW of heat (apart from small losses of energy as infra red, vibration etc.. but let's exclude those for this example as they are negligible).

A 2 kW air source heat pump, when the air temperature around the outdoor unit is 12 °C, will provide 2 kW of heat, but will use in the region of 0.5 kW of electricity to produce that heat.

How is that? I'm aware you can not get more energy out of an action that was put in, but how do air source heat pumps seem to this?

Answer 1

In the traditional efficiency equation the power input is the power to run the compressor motor and the power output is how much mechanical power that motor is producing. In that case efficiency is never greater than unity. But that's not a very useful metric for a heat pump since what you really care about is how much thermal energy that is already there is being moved from one location to another. It's just that in the case of a heat pump, the units for the cargo being moved also happens to also have the units of power. The power output term in the efficiency equation has a different meaning than usual due to intended purpose of the heat pump.

That output power rating for a heat pump is not the power produced by the compressor motor. It is the thermal energy moved by system over time. Whereas the input power rating continues to be energy required to run the heat pump's compressor motor. That's why the metric can have results greater than unity.

A much simpler and straightforward example is you carrying a pot of boiling water into the room versus walking up to a pot of water in the room and using a a muscle powered heater to cause the water to boil. One is far less energy intensive than the other.

If I cared about how much work you did carrying the pot of boiling water into the room, then I would use the traditional efficiency equation. But if I cared about how much thermal energy you brought into the room I would, for the most part, be looking at the energy in the boiling water, not the work you did carrying it in.

Subsequently, if you were using a muscle-powered heater to heat the boiling water, the work you performed and the thermal energy you brought into the room would be the same (ideally).

Answer 2

A heat pump takes heat energy from one side, compresses it a bit (to get to a usable temperature) and transports it to another side.

So you are more or less “stealing” energy from the outside of the house. The assumption is that energy outside of the house is basically free and infinite.

Answer 3

Heat pumps (commonly) use vapor compression cycles (the following is a short summary of a longer article in tlk-energy.de).

To understand this process, you only need the following three key physical relationships:

1. A liquid that evaporates absorbs heat.
2. A condensing gas releases heat.
3. Evaporating/condensing temperature increases with increasing pressure.

By selecting a suitable refrigerant, the following steps are repeatedly performed

1. Evaporate liquid at low pressure and temperature. (Evaporator)
2. Bring the resulting vapor to a higher pressure level. (Refrigerant compressor)
3. Condensate refrigerant vapor at high pressure and temperature. (Condenser)
4. Return the produced liquid to the low-pressure level. (Expansion)

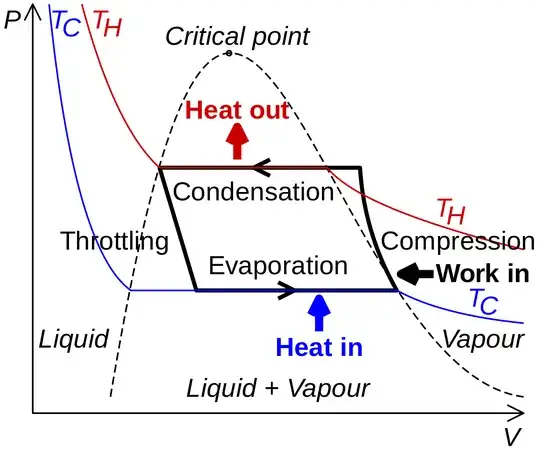
Figure: PV diagram of the refrigerant cycle (source: Wikipedia)

The end result is that the heat energy is taken from a warmer environment and is pushed against the flow to a cooler environment. Because this process is not natural, mechanical work needs to be added during the second step (in the refrigerant compressor).

---

Putting the process in words

Assuming $T_{ce}$ is the cold room temperature and $T_{he}$ is the hot room temperature, then:

Starting with the evaporation step (1), the refrigerant starts with a temperature lower than $T_{ce}$, so it is able to collect heat from the cold room (at the end of the evaporation the temperature is higher but always less than $T_{ce}$); the pressure in this stage is very low.

Then the refrigerant moves into the compressor (2). In this stage, the pressure of the refrigerant is increased (almost adiabatically), and eventually, its temperature also increases and becomes greater that $T_{he}$. Usually, the refrigerant is still in gaseous form (so that the phase change is utilized).

Then at step (3), because the refrigerant's temperature is greater than $T_{he}$, it exchanges heat with the cold room. Usually, at this stage, the refrigerant from the gas turns into liquid.

Finally, in the 4th step, the pressure is lowered, so that it is able to start over from step one (liquid in low pressure).

Answer 4

A very simple answer.

The heat pump has two different parts: inside and outside.

The outside part of the heat pump takes outside air and cools it a few degrees. The heat removed from outside air is then used in the inside part to heat inside air. The net result is that the heat pump dissipates more heat inside than the amount of electrical power used.

This is sort the same as how refridgerator works. Heat is moved from the cold inside the fridge to the warmer outside.

Now, according to normal thermodynamic rules heat does not move from a colder place to a warmer place without a bit of help (and as the physicists knows this statement is a simplification). In this case it takes a bit of technical wizardry. I guess other people are better at explaining the function, but I will do my best. The heat pump (as well as most common fridges and air condition units) uses a carefully selected gas in a closed circuit.

The cycle for the heat pump starts by 1) compressing the gas. When compressing a gas it becomes warmer. This heat is 2) removed by a condenser sitting inside the house. The gas now transfers its heat to the inside air making the house warmer. So far no heat is gained, but next comes the clever part. The gas is moved through a pipe to the outside of the house. It is 3) passed through a small nozzle. The effect is that the gas becomes colder -- when decreasing the pressure the temperature of the gas will drop. This cold gas is now 4) heated by outside air in an evaporator unit. The now heated gas (well heated by outside air so not really hot) is compressed and piped back into the house and the cycle repeats.

The result is that heat is "catched" from the outside and "released" on the inside of the house. The net effect is that the heat pump release more heat inside than what an electrical element using the same amount of electricity would release.

Answer 5

Simply the electricity input drives the compressor which moves the fluid around the system.

The fluid is in one of two states: liquid or gas.

The energy needed to convert liquid to gas and gas to liquid is how the heat energy is moved form one point to another.

That energy moved is greater than the pumping power required. The first systems had a CoP of around 2 ie they moved twice the energy compared to the input energy.

With better quality sensors and computer control as well as precise sizing of components to the task, the CoP now exceeds 4 in many situations.

The CoP is defined as the energy moved from one point to another, so from the evaporator to the condenser divided by the input power to the compressor.

Answer 6

For the same reason that a water pump puts out more water than kW used to run the pump. This analogy is easy to understand because what is being pumped is different than what is powering the pump. In the case of a heat pump both what is being pumped and what is powering the pump are forms of energy.

Answer 7

As mentioned by others, a heat pump transfers heat from one source to another. A heat pump will warm the air through compression, but will remove heat from the outside air in the process making it colder. A resistance heater does not remove heat and instead only generates heat so it takes 2 kWh of energy to produce 2 kWh of heat.

Answer 8

Because the electricity supplied to a heat pump is not part of the core transaction.

You're applying the principles of conservation of energy aka "no free lunch / zero sum game" and noting the "electricity in" bucket does not correspond to the "heat out" bucket. That's correct.

The output heat is not coming from the "electricity in" bucket. It's drawing from a third, totally different bucket - the other condenser/evaporator!

An example

Think of it this way. Suppose your goal is A/C. 10m deep in the ground is plenty of 10 degree C water. You pump that up and run it through a water-air heat exchanger which cools the air. Then you dump the now-20C water somewhere.

The transaction is between the process water and your room air, right? The room air gets cooler and the process water gets hotter and you're taking advantage of this resource of "free" cool water. Fair enough?

Say you're getting 1 megajoule of cooling for negligible cost.

OK, what about the energy used by the water pump? How does that figure into the exchange? Well, it doesn't. It is an incidental or overhead load. So if that pump takes only 20,000 joules, that doesn't really ring any "laws of thermodynamics" alarm bells. It is not a player in the core transaction. You moved 1 megajoule of heat from inside the room to ejected water.

Okay, 1.02 megajoules because the heat energy of pumping probably ended up in the water lol.

Heat pumps are simply doing the same thing but between evaporator and condenser.

Answer 9

Let's say you are blowing air into a beach ball, let's say that when you blow your muscles compress your rib cage by a pressure of 0.01 atm, and the atmosphere compresses your rib cage by pressure of 1 atm.

So 99% of the blowing work is done by the atmosphere.

The "blowing work" equals the increase of the energy of the air that goes into the ball.

Now what energy does the air in the ball have? The air is not moving and no part of the air is stretched or compressed. The only energy the air has is heat energy.

So, that was an example of heat pump where the energy consumption of the motor was 1 % of the heat energy gained.

So is the mechanism of this heat pump understandable?

Well, I think it's difficult to understand.

But, if we do this same thing inside a space station, then it's clear that 99% of the blowing work is done by the heat energy of the air inside the space station, which does not have any other energy than heat energy.

Answer 10

First, think of a gas fired boiler for heating. The gas heats the water and the pump just moves that hot water to where the heat is needed, it doesn’t supply the heat itself. Something similar is happening in a heat pump, except that it uses phase changes in the refrigerant instead for providing the heat.

Start with liquid refrigerant, which has a very low boiling point, (and the reason it’s not a vapor is that it is under high pressure.)
This liquid is sprayed through a small nozzle into the evaporator, which is located outside. The refrigerant vaporizes, (the pressure here is low) and cools. As it changes state from liquid to vapor it needs to absorb energy (latent heat of vaporization), which it does by transferring heat from and cooling the outside air. The refrigerant vapor now has a much higher heat content than the liquid had, but all this heat came from the outside air.

The compressor then compresses this vapor, which heats it, maybe to about 200°F . This is the only work the compressor does.
The compressed vapor travels to the condenser (inside the house). In the condenser the relatively cool air cools this vapor to perhaps 90°F, at this temperature and pressure the vapor condenses, giving up its latent heat to the air stream.

The warm high pressure liquid refrigerant returns to the evaporator where the cycle recommences.

In the condenser the vapor gives up heat - the heat of compression and its latent heat.
The COP (coefficient of performance) is$$\frac {heat\ delivered}{work\ done\ by\ compressor} = \frac{work\ done\ by\ compressor + latent\ heat\ of\ refrigerant}{work\ done\ by\ compressor}$$ which is usually greater than 1. COP of 6 is not unusual.

Answer 11

There are already many correct answers, but they fail to mention a point which is one of the causes of the confusion. The nice scenario applies only under certain conditions. The flat statement, that the heat pump will output an amount of heat that is equivalent to more than the energy required to power it, is false if you do not have a source (or an accumulator) of heat close at hand.

The overwhelming majority of the houses in the USA are small homes with access to their underground. They may use it to accumulate heat during the Summer and recover it during the Winter. But not all the places have a suitable underground and outside the US the proportion of isolated homes is way smaller. The US citizens tend to ignore the outside world and just state: "if it is this way in my home then it is the same all over the world". But actually the majority of the heat pump installations throughout the world have an efficiency comparable to the classic air conditioners.