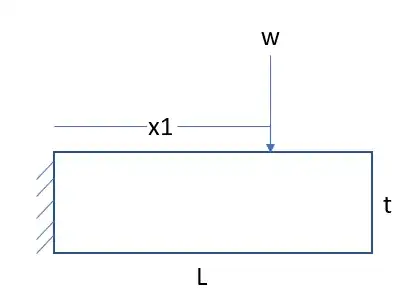
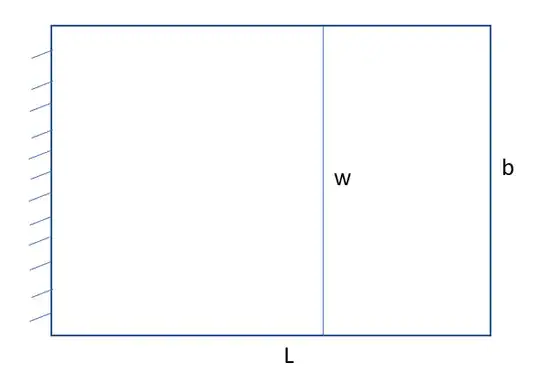
Does any one happen to know of any resources that describe the stress and displacement of a uniformly distributed load in the direction perpendicular to the length direction of a plate analytically? I have checked both Roarks Formulas for Stress and Strain and Plates and Shells Theory and Analysis by Ansel Ugural and I do not see anything quite what I am looking for. Hopefully the images below help.
For bending of wide plates, we typically use the so-called plane-strain modulus $\frac{E}{1-\nu^2}$, where $E$ is Young's modulus and $\nu$ is Poisson's ratio. For $\nu=0.3$, for example—typical for ductile metals—the plate is predicted to be 10% stiffer than a narrow beam.
The reason is that the narrow beam is free to expand laterally on the compressive side and contract laterally on the tensile side, both due to Poisson effects. Because of the nearby free surfaces on either side of the width, the lengthwise cross-section is considered to be in a state of plane stress; lateral deformation is unencumbered. (This can be a point of confusion: Recall the Poisson effects aren't driven by external lateral stress; they occur freely because of the lack of an external lateral stress.)
This isn't the case with the wide plate, whose cross-section is instead in a state of plane strain (minimal strain allowed in the width direction). Now those Poisson effects are suppressed by an internal strain (in the width direction) acting on most of the lengthwise cross-sections (the $L-t$ plane in your diagram). As is typical, any extra constraint makes the material stiffer, and correspondingly $\frac{E}{1-\nu^2}>E$.
I derive various moduli in a page on generalized Hooke's Law (in progress) here. Briefly, generalized Hooke's Law
$$\varepsilon_{ij}=\frac{1+\nu}{E}\sigma_{ij}-\frac{\nu}{E}\delta_{ij}\sigma_{kk}$$
couples the 3-D strain $\varepsilon_{ij}$ and stress $\sigma_{ij}$ in isotropic materials. (Simple Hooke's Law $\sigma=E\varepsilon$ strictly applies only to axial loading of long, thin bars.) Here, $\delta_{ij}$ is 1 if $i=j$ and 0 otherwise, and $\sigma_{kk}=\sigma_{11}+\sigma_{22}+\sigma_{33}$. With $\varepsilon_{33}=0$ for plane strain and $\sigma_{11}$ loading, we have $\sigma_{33}=-\nu\sigma_{11}$ (the widthwise stress that arises because the wide plate can't easily shrink on one side and expand on the other), and thus
$$\varepsilon_{11}=\frac{1-\nu^2}{E}\sigma_{11},$$
whereas the plane-stress case would instead yield $\varepsilon=\frac{1}{E}\sigma_{11}$.
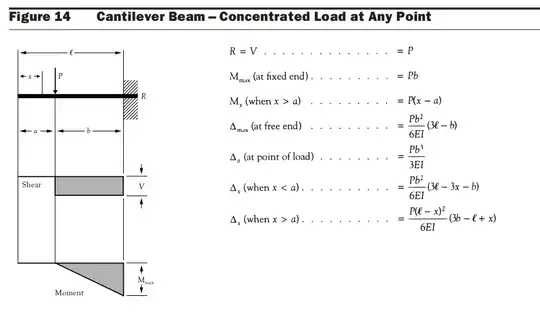
If you are after the deflection of the beam at any point along the beam (but also for most intends and purposes - see below for exceptions) the problem you are after is equivalent to the following 2D case.
The concentrated load at distance $a$, can be considered as applied to the entire width of the beam, so no asymmetry is present in the system. Then you can go to a table from a resource like Design Aid 6 and get the equations
Notable exceptions would include the following:
There might be others cases, but I already consider the above cases too exotic and unusual to be encountered, in engineering calculations that would be expected to be solved with closed form solutions.
