Conditions: there is a steel plate insulated at the bottom and facing the clear night sky, the ambient air temperature is 2°C, the cosmic microwave background radiation is 3K, and the convective heat transfer coefficient is 10 
. My job is to calculate the temperature of the steel plate at thermal equilibrium. The steel plate doesn't have given dimensions.
I've used 
for the convective heat transfer, and 
for the radiative heat transfer. Using 0.8 as the emissivity of steel, 
yields -22.158°C which is close enough to the textbook's answer of -20.9°C. This textbook has provided wrong answers multiple times in the past, so I don't fully trust it and this answer doesn't seem right to me.
Attempts to calculate in Kelvin have resulted in even more unlikely answers. Is -20°C plausible? Or where did I go wrong?
Edited to add calculations:
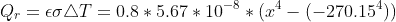
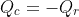
My calculator puts out:
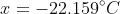as the solution.
