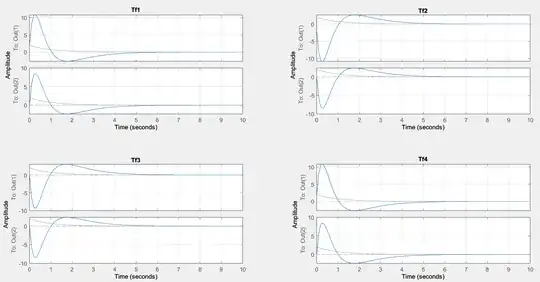
I am currently working on a MIMO feedback system and trying to determine its internal stability. The open loop gain of the system is stable and has no internal right half-plane pole-zero cancellations. The closed-loop feedback system has 4 closed-loop transfer function matrices, and I have checked the stability of all of them one by one using an arbitrary decaying input.
As can be seen, all 4 closed-loop TFs are stable, which means the closed-loop system should be internally stable. Now, I tried to verify this conclusion using the small-gain theorem, and to do that, I picked a frequency range and calculated the upper singular value of the open-loop gain at each frequency.
The upper singular values of the open-loop gain go above 1, which means the h-infinity norm of the open-loop TF will also be greater than 1, which according to the small gain theorem, implies internal instability of the closed-loop system, which is not the case.
I recognize that the small gain theorem is only a sufficient condition for internal stability, so there must be another condition that I am missing. I wanted to know where is my analysis lacking.