I am a novice in automatic control, the theoretical basis is not very good. We have a large electric clamping jaw, single degree of freedom, the motor is controlled by the torque output, the motor has a maximum stable clamping stiffness (This parameter is related to the gain margin, the greater the gain margin the greater the clamping stiffness can be). There is a rigid coupling between the motor and the gearbox.
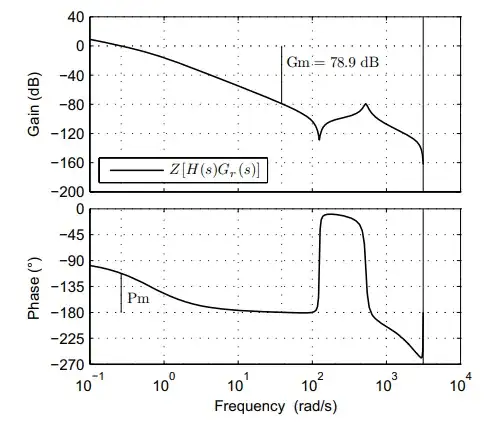
We simulated the Porter diagram of the motor with matlab and got the curve shown in the first diagram, Gm is 78.9dB.
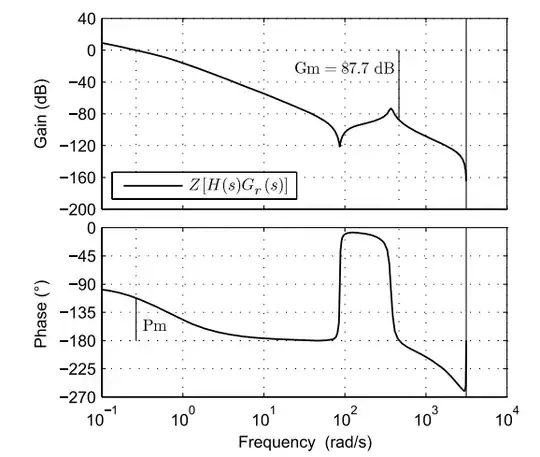
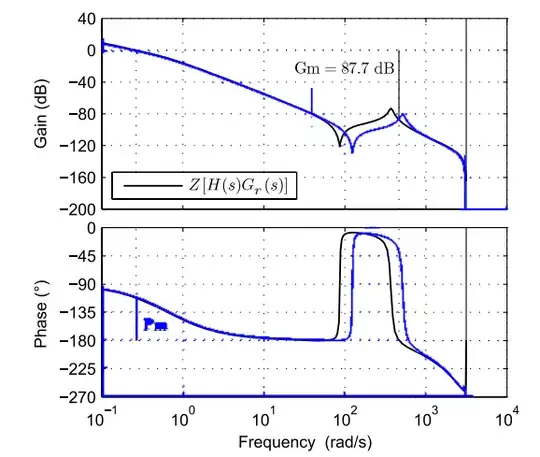
Then we changed the coupling to a flexible (elastic) coupling and got the second diagram below, Gm became larger, 87.7dB. My question is, when the coupling is changed to flexible, intuitively I feel it will cause resonance. But why is the gain margin bigger instead. Also, the part of the Gm increase appears a little to the right of the peak resonant frequency. Does this resonant frequency have any effect on stability?
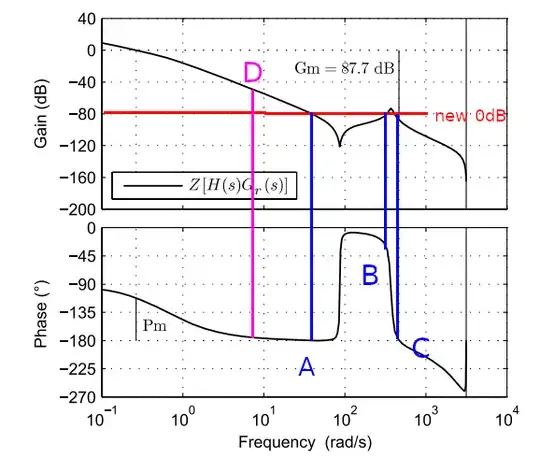
In addition, there is another question. For the above figure, the gain margin of 87.7, when I set the maximum gain to 87.7 near the stability will become worse, or that the frequency of my control signal reaches the resonant frequency when the stability will be affected