5 balanced masses on wheel with different distances between them

Question

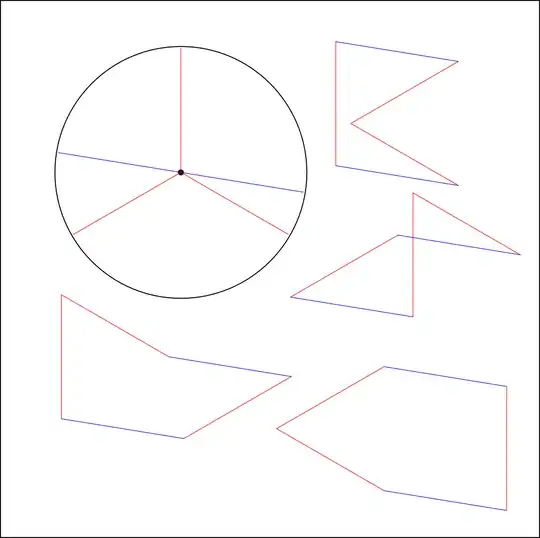
I'm looking for a way to calculate possible balanced positions of 5 equal masses on the circumference of a spinning wheel such that the distance along the circumference between the masses are all different, and no distance is an integer multiple of any of other the other distances. This is like the balanced centrifuge problem, but without defined slots.

Masses arranged in a 5 point star would be balanced, but the distances would all be the same. 3 masses in an equilateral triangle with 2 additional masses places across from each other would also be balanced, but distances between the 3 masses would be the same, and the distances between the 2 are the same clockwise and counter clockwise. Is there a possible arrangement of 5 masses where all the distances are different?

Answer 1

You need to draw a vector diagram of the unbalance force due to each of the 5 masses. Put each vector nose to tail and if they come back to the origin then its balanced. An easy way to think about this vector chain is a chain with 5 equal length links in a loop. Any of its infinitely many configurations is balanced.

Answer 2

Based on Greg Locock's answer I made this diagram that starts off with a balanced arrangement and then I moved the vectors to create these pentagons. This particular balanced arrangement doesn't meet the criteria that the distances be non-integer multiples of other distances, but this is definitely a step closer to the solution I'm seeking.

Here is a diagram of fixing two of the vectors (black arrows) and moving the other vectors (red arrows) to find a new balanced arrangements.

Answer 3

There are infinite positions that will qualify for the balance.

Let's assume we suspend a wheel of radius 1 from its center with 5 equal masses P from a string.

An easy answer is to put the masses at the corners of a pentagon with the top corner at point A(0, 1) and annotating counterclockwise,B at 90+72 = 162, thus B (cos 162, sin162)=B(-0.951, 0.309) ; C(-0.587,-0.809): D(0.587, -0.809); E (0.951, 0.309).

Now we move points C and D down by a random amount, say 0.02 to the new ordinate y=-0.809 -0.02=0.829. The abscissa will change following $sin^2+ cos^2=1$ but we are not concerned with that.

All we need to do is move B and E up to the new elevation of Y2. Due to the symmetry, we don't worry about changes in x coordinate.

For the centroid to pass through the origin.

$$ Y_o= 0 =\frac{1*p+2Y_2*p-2p*0.829}{5p}$$ $$p+2Y_2p-1.658p=0$$ $$p(1+2Y_2-1.658)=0$$ $$2Y_2=0.658 \quad Y_2=0.329$$ The fact that the change in the ordinate of the B and C are equal is due to rounding of arithmetic, normally they aren't.

When the wheel is balanced about the Y axis and the X axis, it is in polar balance.

We could repeat this by turning the wheel to B at the top, etc.

There are many other configurations, such as perturbing 1, and 2, or3 points.