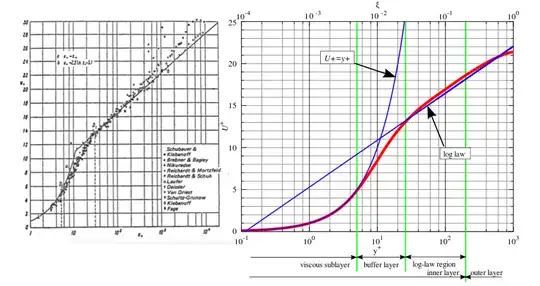
According to Hoffman, the standard $k-\epsilon$ turbulence model incorporates a two-layer approach (inner region and outer region formulations to reperesent mixing length) when it comes to regions adjacent to wall surface $(y^+ \approx 30 - 50)$.
My understanding of the $k-\epsilon$ model is that a two additional equations are added to the system of flow governing equations, one equation for kinetic turbulence energy $k$ and the other is for the turbulence energy dissipation rate $\epsilon$, and the closure problem is solved by using dimensionless groups as boundary conditions such as turbulence intensity, turbulence length scale and hydraulic diameter.
My question is why the $k-\epsilon$ model uses zero equations models (algebraic models) for regions adjacent to the wall, what advantages do zero equations models have over $k-\epsilon$ if by definition zero equations models assume that the rate of production of turbulence and the rate of dissipation are approximately equal and they do not include the convection of turbulence?