Maximum tensile and shear loads on screw

Question

I'm using a screw in an application where I want to have a high degree of confidence the screw will not fail, and I want to be sure I'm calculating the maximum tensile and shear loads it can sustain correctly as well as the tension and shear it's exposed to.

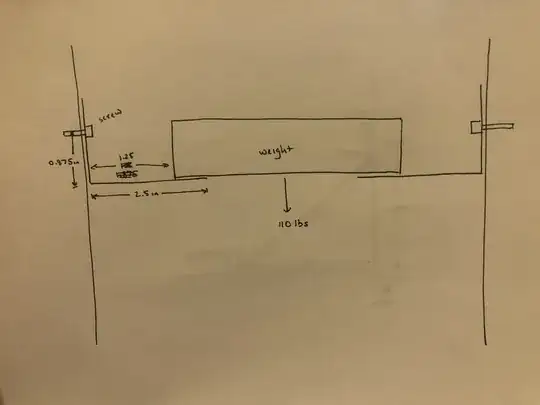
The following description is depicted in the attached image. A 100lb weight is shared between two rails. These are 2.5x1.5, 3/16" thick L angle galvanized steel. Each rail is fastened to a wall with 2 screws (the second screw is behind the first and not shown in the image). The weight overlaps each rail by 1.25in. If we assume the weight is equally shared between both rails then we can consider the 55lb force as being applied downward on the rail at a point 1.875in from the wall. The two fasteners each provide the compensating upward force 27.5lb each. The force of the weight on the rail creates a torque on the rail where the r vector points from the screw attachment point to the point on the rail where we consider the force as being applied (ie 1.875in from the wall). Using rFsin(theta), the magnitude of the torque should be about 103in-lb. The wall pushes on the vertical portion of the rail to counter that torque (and prevent rotation). If we consider all of that force as being applied to the rail corner (this should be overly pessimistic), the requisite force to counter the torque is a total of 118lb. The two screws should share that force, so 59lb each. So, the tension on each screw should be 59lb and the single shear on each screw should be 27.5lb.

The screws are M6. Considering an effective diameter of 5.35mm (0.035in^2 area), and a tensile strength of 80k PSI that should support a tensile load of 2800lb. If we consider the shear strength to be 60% of the tensile strength (apparently that's reasonable - is it?), then it should support a shear load of 1680lb. That puts us way below the rating.

Is this process correct and are the rough calculations reasonable? Anything important I'm failing to consider? The walls are not actually ideal walls, but instead the mounting posts of a 19-inch rack, but they should be quite sturdy.

My main hope with this post is to get a basic understanding of how to calculate screw loads and strengths.

Answer 1

Its a bit hard to follow what you are doing. You should use LaTex to write your calculations.

The tension on the screw:

$100lbs/2=50lbs \quad \text{half wight of the load }$

$50/2=25lbs \ \text{share of each screw}$

$Torque= 25lbs*1.875in=45.875\#in$

$Tension_{screw}=\frac{Torque}{lever arm}=\frac{46.875}{0.875*2/3}=80.357lbs$

Note: lever arm is the distance from CG. of wall traingular stress block to the screw. The rest of your calculations seem correct.

We have to check distance from the holes to the edge of the angles and check the strength of the sopport wall. We have to apply appropriate safety factor and load combinations.

Answer 2

Bolts are not supposed to fail in shear. Bolted connections should be sized such that the preload applied to the joint and friction between mating surfaces handles the shear load. Preload is typically specified as somewhere between 60% and 80% of yield strength. The preload only acts on the bolt in tension. In your particular scenario you will have and additional tensile load to counter the moment on the bracket. What that moment actually is for you is dependent on how the weight is distributed on the bracket. Worst case for you is concentrated load at the end.

This will be (110lb * 2.5in)/0.875in/2 = 157 lb per bolt group (assuming they are at the same horizontal level, otherwise the math is a little different and you assume the tension for each bolt is proportional to the distance from the pivot point, which is the bottom of your bracket). You should add an appropriate safety factor to that number when sizing your bolt.