External diffusion: calculation of surface concentration

Question

I am struggling a bit with an external diffusion problem. I am trying to calculate the concentration at the surface (as well as surface reaction rate) and would like some help or guidance.

Here is what I have thus far.

The reaction taking place, is

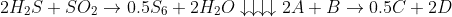
I want to calculate the concentration of B at the surface of a spherical catalyst particle.

Flux:

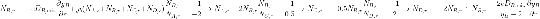
Now, from the diffusion equation:

.

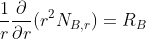R_A can be approximated by the first order reaction rate

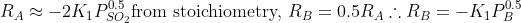
so

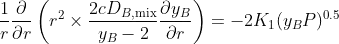
(just ignore the "2" after the =)

Now, the boundary conditions that I think I should use, are

Note, at all times, I already have the values of all components' bulk concentrations, and I also have values for D_i,j and D_i,mix for all i,j.

Are my boundary conditions chosen correctly for solving for the surface concentration of B (i.e. c_B or y_B or P_B, which are all related)?

Edit:

I need surface values for calculation of the effectiveness factor. I can use any way to calculate surface values with the values that I already have.

I chose r to be any point in the radial direction, even "past" the sphere (when going from r=0, the centre), delta = the thickness of the boundary layer.

Edit 2:

It seems I may have over-complicated it. Based on this video, the control volume considered is only the gas part - the boundary layer. This is correct, since the reaction is assumed to only take place on the catalyst surface and not in the gas phase itself.

In that case, $R_B=0$

$\therefore \large{ \frac{\partial }{\partial r}\left ( r^2 \frac{2cD_{B,\text{mix}}}{y_B-2} \frac{\partial y_B}{\partial r} \right)=0}$

So, at $y_B(0)=y_{B,\text{surf}}$ and $y_B(\delta)=y_{B,\text{bulk}}$

!! Ahh, I've just realized a mistake in my boundary conditions. At $r=0$, we are at the center of the sphere, so that boundary condition is incorrect. !!

So, let's try again:

At $y_B(r=r_{sphere})=y_{B,\text{surf}}$ and $y_B(\delta)=y_{B,\text{bulk}}$

From Matlab: $\large{y_B= 2+{\left (y_{B,\text{bulk}}-2 \right )} \left ( \frac{y_{B,\text{surf}}-2}{y_{B,\text{bulk}}-2} \right )^{\left (\frac{r_{\text{sphere}}\left ( \delta -r \right )}{r\left ( \delta -r_{\text{sphere}} \right )} \right )} }$

Now what? How do I get the surface concentration values? Since I do not know the thickness of the boundary layer ($\delta$)?

Answer 1

The way you have solved your problem you have treated the concentration at the surface of the sphere as known ($y_{B,\text{surf}}$). Notice that in your final answer, if you plug in $r=r_\text{sphere}$ all you will get is $y_{B,\text{surf}}$. Instead, your boundary condition at the surface should be something like this:

$$ N_{B,r}=-K_1P_B^{0.5}=-K_1y_B^{0.5}P^{0.5} $$

Here you are equating the flux at the surface of the catalyst particle (where the reaction is happening) to the reaction rate. Rearranging you can write that at $r=r_\text{sphere}$, $y_{B,\text{surf}}$ is:

$$ \left(\frac{N_{B,r}}{-K_1P^{0.5}}\right)^{2} $$

Now you could solve the problem to find the value of $N_{B,r}$ which is constant at steady state according to your equations. You may get a transcendental equation of $N_{B,r}$ that requires numerical or graphical solution.

One caveat, this is all based on a film-model of mass transport and heterogeneous reaction. It means that you will need some experimental data to correlate the rate of reaction to the thickness of the film model, $\delta$.

Answer 2

If we can assume the sphere has a radius $r_0$, and that $\delta$ is the thickness of the boundary layer surrounding the sphere, then the boundary conditions I would use are

$$y_B(r= r_0 + \delta)=y_{B,bulk}$$ $$\frac{\partial y_B}{\partial r} \bigg|_{r=0}=0$$

The first one (Dirichlet boundary condition) is what you have already. The second one (Neumann boundary condition) is due to the symmetry of the spherical particle.

However, the diffusion through the boundary layer will be a separate equation from the diffusion through the sphere. You'll need to set some kind of continuity condition so that the two solutions produce the same value of $y_B$ where they intersect at the surface of the sphere.