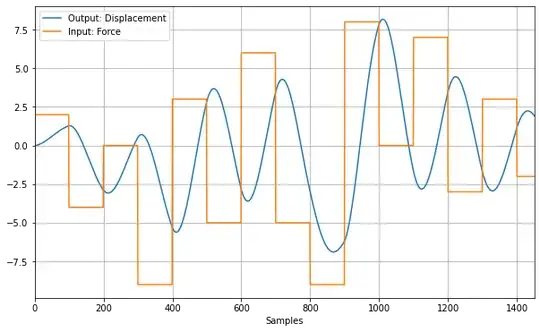
I have been trying to identify a simple linear second order system (e.g. a pendulum or a mass-spring system), by simulating it in Python using backwards-euler method and then feeding the step changes in force as Input (x) to simple RNN network, and recorded Position (y) as an output. It is assumed that Driving Force from the timestep t-2 correlates with Displacement in timestep t.
Since model has two states I have used RNN with only two hidden units (states)as this structure is equivalent to state-space description of linear system and should be sufficient to represent the behavior of the system (as discussed here and described in more details here here). Further more, since the relationship between inputs-states-outputs is linear, only linear activation functions are used.
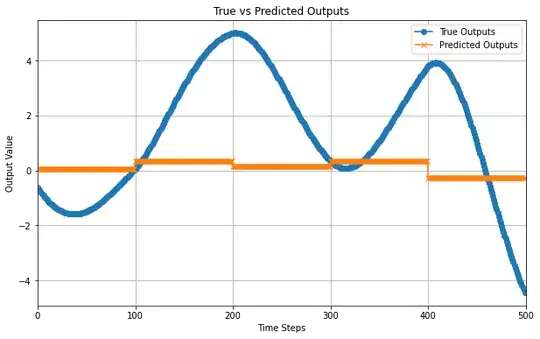
Interestingly enough, solver is for some reason not able to fit the NN to match the output from the training/validation set, and as you can see below, seem to only "feed-thru" only the step like input changes, whereas the oscillatory effect that is supposed to come from the interaction between the states (velocity, position), is not captured.
(Note: Larger networks of 32 units as well as LSTM have been used, but still with poor results, indicating problem is elsewhere. Training and validation error are both barely reducing within first 250 epochs)
Network is described by the code below:
model=Sequential()
model.add(SimpleRNN(units=2, activation='linear', input_shape=(len(Input), 1),use_bias = False)) model.add(Dense(1,activation='linear', use_bias = False))
model.compile(optimizer='adam', loss='mse')
model.summary()
And fit using:
model.fit(X_train, y_train, epochs=500, validation_data=(X_val, y_val))
Training data and the results are shown on the following images:
Image: Training Input-Output data recorded from the state-space model
Image: Totally incorrect prediction output
I have managed to fit the model perfectly using Feedforward neural network with same ammount of units, giving as input vector of current input and previous two states as follows: [Input(t) Output(t-1) Output(t-2)]. (something like ARX model)
It seems I am missing something about the structure of RNN and the data format they expect.
Also model.get_weights() produces following output, not sure how to interpret it exactly:
[array([[-0.29872632, -0.17957304]], dtype=float32), array([[ 0.8877555 , -0.46031553], [ 0.46031553, 0.8877554 ]], dtype=float32), array([[-0.73704493], [ 0.8689412 ]], dtype=float32)]