Buckling: Do buckling mode shapes of n > 1 occur in reality?

Question

In the buckling of columns we know that:

$$P = \dfrac{n^2\pi^2EI}{L^2}$$

The smallest value of P occurs when $n=1$ which gives a simple buckling shape (one wave):

$$P_{cr} = \dfrac{\pi^2EI}{L^2}$$

However for $n > 1$, as shown below the buckling shape is more complex and has many waves:

My question is do the buckling mode shapes for $n > 1$ ever occur in reality? If the column begins to buckle as per the shape for $n = 1$ then wouldn't it just continue to buckle like this until failure? How would the other buckling modes ever occur?

Answer 1

If you are looking at the column as being supported at the ends, you are correct that the n=1 mode gives the lowest buckling load.

The other modes (n=2,3,...) aren't useless though. Long columns are often braced at regular intervals to reduce the unbraced length of the column. For a given length of column, these braces force the column to buckle under a different mode (n=2,3,...) with the corresponding increase in buckling load.

Answer 2

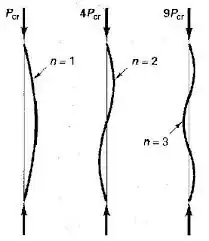
Whether or not buckling modes with $n>1$ exists depends on how you look at the structure.

As @hazzey notes in his answer, columns with bracing may display buckling modes with $n>1$. These buckling modes, however, are simply equivalent to the $n=1$ modes of the individual segments that compose the column. To be clear, this doesn't mean that the segments behave independently (you'll never have two consecutive unbraced lengths buckling to the same side), only that any $n>1$ mode can be composed by a series of continuous $n=1$ modes for the unbraced lengths.

So, if you have a column with a single bracing which buckles, do you consider that an $n>1$ mode for the entire column or an $n=1$ mode for each of the unbraced lengths? Both? Your call.

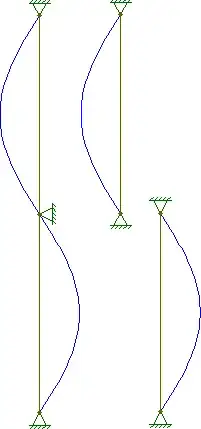
To paraphrase @starrise's comment on @hazzey's answer, this can be demonstrated by looking at the buckling equation: \begin{align} P &= \left(\dfrac{n}{L}\right)^2\pi^2EI \\ P_{column,\,n=2} &= \left(\dfrac{2}{L}\right)^2\pi^2EI \\ P_{segment,\,n=1} &= \left(\dfrac{1}{\frac{L}{2}}\right)^2\pi^2EI = \left(\dfrac{2}{L}\right)^2\pi^2EI \\ \therefore P_{column,\,n=2} &= P_{segment,\,n=1} \end{align}