Stability of a closed-loop with disturbance in output. Characteristic equation alone or substitution

Question

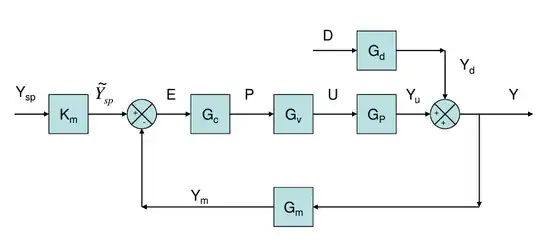
A general block diagram of a feedback controlled process with a disturbance in the output is:

If we assume that the following blocks are equal to 1, and therefore we remove them:

$$ K_m = G_v = G_m = 1$$

We have the following expression in frequency domain:

$$Y = G_dD + G_pG_c(Y_{sp} - Y)$$

If we rearrange this we reach:

$$ Y = \frac{G_pG_c}{1+G_pG_c}Y_{sp} + \frac{G_d}{1+G_pG_c} D$$

All books insist that to check stability, we have to check the roots of the characteristic equations alone, i.e., the roots of $1 + G_pG_c$, since this appears in both denominators. However, shouldn't we also check the actual numerators? For example, if the disturbance is unstable, and:

$$G_d = \frac{1}{s-1}$$

Then the system is not stable at all. It does not matter what the roots of $1 + G_pG_c$ are, since we are adding a positive root to the denominator. It would be: $$Y = \frac{G_pG_c}{1+G_pG_c}Y_{sp} + \frac{1}{(s-1)(1+G_pG_c)} D$$ The literature i've seen always refers only to the characteristic equation and not the numerator... is there a reason for this? Shouldn't we always substitute the transfer functions first?

Answer 1

For example, if the disturbance is unstable... Gd = 1/(s-1)

In that case, the (s-1)^(-1) would be part of the denominator after simplification; and hence part of the characteristic equation.

The literature i've seen always refers only to the characteristic equation and not the numerator.

No, $G_d$ is a ratio of polynomials and itself contains a numerator and a denominator. The denominator needs to be shifted to the main denominator.

e.g.

$$ \frac{(s+1)/\color{red}{(s+4)}}{(s+2)/(s+7)} = \frac{(s+1)(s+7)}{\color{red}{(s+4)}(s+2)} $$

All books insist that to check stability, ...

If they are well written books, they will most likely contain some fine print at the beginning of the chapter or some kind of foot note that says something like: "The individual blocks in the block diagram are assumed to be stable systems". Since you have not given a specific (reputable) reference text book, it not possible to know what the author's stated assumptions were.