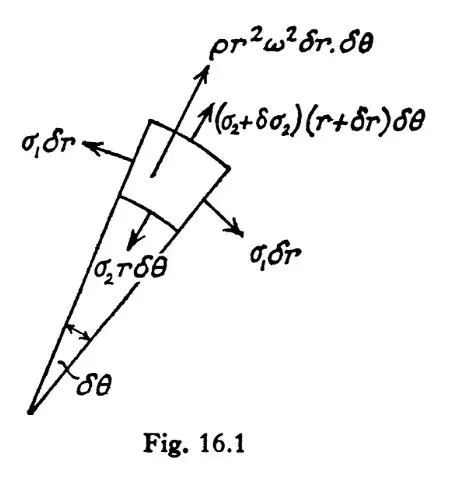
I use this model to get the tangential and radial stress formulas but I want to examine a system also undergoes a torsion under constant speed. I'm a little confused at this point, do I need to point out the torsional stress in this picture and calculate all the formulas according to it, or do I need to just sum the results?
$ \sigma _ {1} =( \rho \omega ^ {2} /8)[(3+v)( R_ {1}^{2} + R_{2}^{2} + R_ {1}^ {2} R_{2}^{2} /r^ {2} )-(1+3v) r^ {2} $ ]
$ \sigma _ {2} =(3+v)( \rho \omega ^ {2} /8)( R_ {1}^ {2} + R_ {2}^ {2} - R_ {1}^ {2} R_ {2}^ {2} /r^ {2} - r^ {2}) $