Why do period and damping ratio affect acceleration?

Question

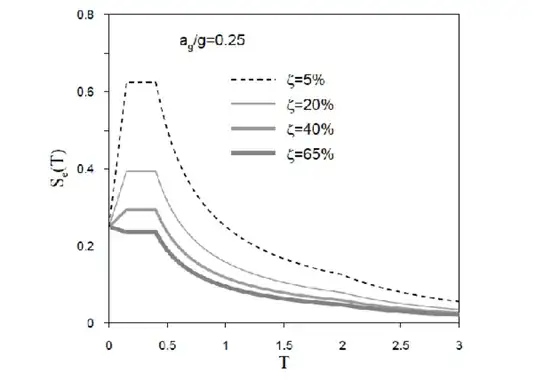
In the table above, the period of the structure $(T)$, the acceleration coefficient on the structure ($g$ in terms of gravitational acceleration) $Sa(T)$, The damping ratio is expressed as $ζ$ .

As the damping ratio of a structure increases, the earthquake design acceleration on the structure decreases. That's why the earthquake force is decreasing. But how can damping change the amount of an external force? In other words, why does the damping ratio cause the earthquake design acceleration of a structure to decrease? We know that as the period of the structure increases, the earthquake force on the structure decreases. Can you explain the theoretical reason for this? Am I misunderstanding the nature of the earthquake force?

Answer 1

The goal in designing structures to resist earthquakes is to prevent resonance of the building vibration with ground vibration. Two ways to achieve this are to design for a natural frequency of the building not too near to the expected ground frequency and increase the damping.

By checking the equation of forced vibration below, we see the greater the damping, the more ground motion energy is absorbed by damping, and less is available to accelerate the building!

$$ m y''+cy'+ky=F_0\cos(\omega t),\quad y(0)=y_0,\quad y'(0)=v_0. $$