Does moving the idler in a wheel and disk CVT conserve energy or momentum?

Question

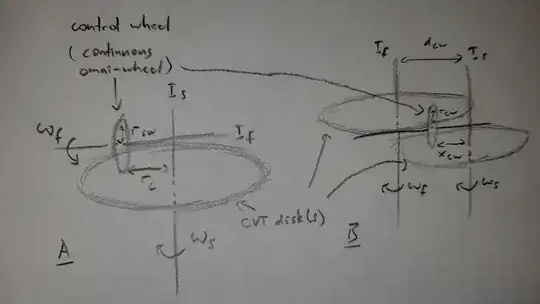
Consider the wheel and disk CVTs (continuous variable transmissions) below. Configuration A comprises a CVT disk coupled to the "system under control" 's', whereby a control wheel 'cw' constructed from a continuous omni-wheel engages with it perpendicularly, translating left and right with minimal resistance (assume no friction in this case), its being coupled to a flywheel 'f'. Let 's' and 'f' have effective moments of inertia $I_s$ and $I_f$, whereby the angular velocities are related by $\omega_f=\frac{r_c}{r_{cw}}\omega_s$; for Configuration B which alters the input and output rotation axes to be parallel, $\omega_f=\frac{-x_{cw}}{d_{cw}+x_{cw}}\omega_s$.

I wish to analyze the dynamics of the momentum transfer from moving the control wheel (i.e. for $\omega_f=\frac{vt+r_{c0}}{r_{cw}}\omega_s$ in Configuration A or $\omega_f=-\frac{vt+x_{cw0}}{d_{cw}+(vt+x_{cw0})}\omega_s$ in Configuration B where $v \neq 0$ and $t >= 0$), whereby I am unclear on whether this system is supposed to conserve rotational kinetic energy or angular momentum. As you will see below, my present attempts lead to only one or the other being conserved.

• In conserving momentum (solving for $\omega_s$ in $L_{T0}=I_s\omega_s+I_f\omega_f$), I would find it most odd that the motion of the control wheel without a reaction force beyond the control wheel's own translational inertia would impart work on the system mind incur a vertical asymptote.
• In conserving energy (solving for $\omega_s$ in $E_{T0}=\frac{1}{2}(I_s\omega_s^2+I_f\omega_f^2)$), though the predictions of angular velocity and acceleration with respect to time are more sensible, I find it unclear whether we should expect the dynamic changing of the CVT ratio to impart a net change on the system's angular momentum.

To show how I arrived upon these disparities, I have provided https://www.desmos.com/calculator/n8aypfivci and https://www.desmos.com/calculator/wqncpali6t which contain interactive graphs of my equations for Configurations A and B, respectively:

• In each, the first folder contains sliders for the parameters with descriptions; the second folder models the system assuming conservation of energy; the third folder models the system assuming conservation of momentum (I admit I may have not properly set up the total angular momentum for orthogonally rotating bodies for Configuration A, but a similar disparity is found with the Configuration B calculations).
• One can click on the folder icons to show and hide the curves for conservation of energy and momentum, respectively. The green curve is the total rotational kinetic energy. The blue curve is the total angular momentum (likely incorrect in Configuration A, but likely correct in Configuration B). The orange curve is $\omega_s$. The red curve is $\omega_f$. The purple curve is the angular acceleration $\alpha_s$.

This question was moved from https://physics.stackexchange.com/questions/818720/does-moving-the-idler-in-a-wheel-and-disk-cvt-conserve-energy-or-momentum.

Answer 1

I have realized that these systems do in fact conserve both rotational kinetic energy and angular momentum, whereby what I had not considered was the rotation of the entire CVT system itself, or that in practice, this system would have been coupled to the entire inertia of the Earth (or whichever large object it is affixed to).

• For Configuration A, the angular momentum vectors form a diagonal vector toward the lower left, whereby as the control wheel's motion causes this vector to move, the angular momentum vector of the combined system will cancel out this change, causing the entire CVT assembly to rotate diagonally.
• For Configuration B, translating the control wheel would have induced a horizontal rotation of the entire system.
• I have updated the Configuration B Desmos graph in https://www.desmos.com/calculator/xbfmkbsbps to include the kinetic rotational energy and angular momentum of the entire CVT assembly about its center of mass. In line 50, you can move the $I_E$ slider to see how the dashed orange curve approaches the solid orange curve. In line 55, you can see how after carrying the left $I_E$ over to the other side, as $I_E$ approaches infinity, it approaches the equation seen at line 57 from which line 58 is easily derived. Finally, in lines 67 and 68, you will see that both the summed up rotational kinetic energy and angular momentum are conserved and remain constant with time regardless of the value of $I_E$.