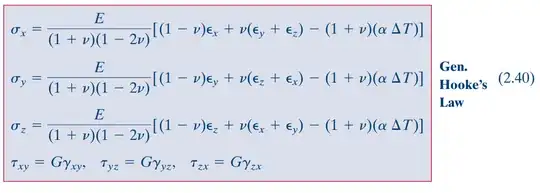Interpretation of the generalized Hooke's law

Question

I'm in the process of understanding the generalized Hooke's law for an isotropic, linear-elastic material. I've come across two formulations of the same low in Mechanics of Materials by Roy Craig Jr., which are described below.

Let's get the x components, and let's assume $\sigma_y = \sigma_z = 0$, also that there is no temperature gradient. From Eq. 2.38 we then get $\sigma_x = E \cdot \epsilon_x$. However, 2.40 gives $\sigma_x = (E(1-\nu)/(1+\nu) \cdot (1-2 \nu)) \cdot \epsilon_x$, which clearly is not the same thing.

What am I missing here?

Answer 1

You missed the lateral contraction. In addition to normal strain in the $x$ direction, there are lateral contractions in the $y$ and $z$ directions.

$$\large\epsilon_y=\epsilon_z=-\nu\epsilon_x\tag{1}$$

Substituting these values in the second formulation (2.40), we get $$\sigma_x=\frac{E}{(1+\nu)(1-2\nu)}\left[(1-\nu)\epsilon_x+\nu(-2\nu\epsilon_x)\right]=\frac{E}{1-\nu-2\nu^2}\cdot(1-\nu-2\nu^2)\epsilon_x=E\epsilon_x\qquad\text{proved.}$$ which is the same as $\sigma_x$ in the first formulation (2.38) of the generalized Hooke's law for an isotropic, linear-elastic material.

I hope this helps!