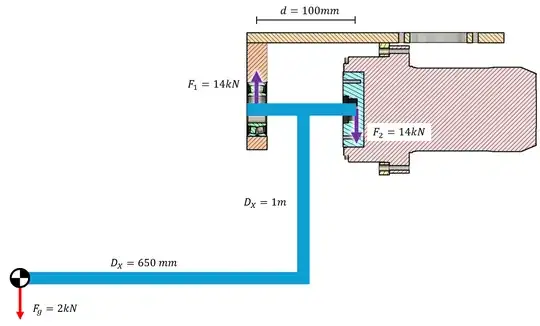
I'm not a mechanical engineer, but I've been tasked with designing a system that uses a harmonic drive motor (specifically, a LynxDrive). It must rotate a 200kg mass, which is heavily off-center. It only needs to move a few degrees clockwise and counter-clockwise. Here's a simplified diagram:
$F_g$ is caused by the mass, and exerts a moment on the motor+bearing assembly. I've selected a spherical roller bearing to avoid misalignment issues, while the motor has a cross roller output bearing. If the moment is split equally between the two bearings, and my math is correct, each bearing is subject to a radial load of ~$14kN$. I'm not sure about the 50/50 force split, because -I suppose- the most rigid bearing of the two will take more load that the other. Feel free to correct me on that.
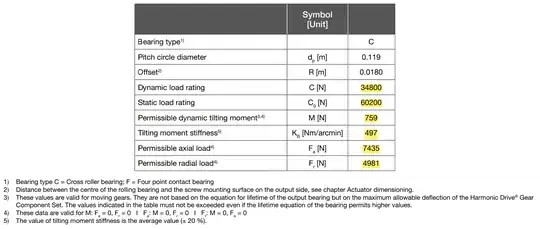
My doubt is on the specifications of the motor bearing. I undertand that the dynamic load is only useful for estimating the L10 life, while the static load rating is the load that causes a 0.01% deformation of the rollers and raceways in the motor's bearing. Simple bearings only provide those two specifications, while this motor also has a "permissible radial load". Why is it so much lower than the $C_0$ rating? As for the what this permissible load is, I've read that it's $C_0$ divided by a safety factor, but then it isn't clear to me why the manufacturer assumed such a big safety factor. Perhaps because this motor is used for robotics? Should I not care about the permissible load then?
If, instead, I must stay below the permissible radial load, what do you recommend to do? I haven't found in literature a bearing arrangment that could work (there would be 3 distinct bearings, over-constraining the shaft, right?). There is a high risk of mis-alignment between the 3 bearings.