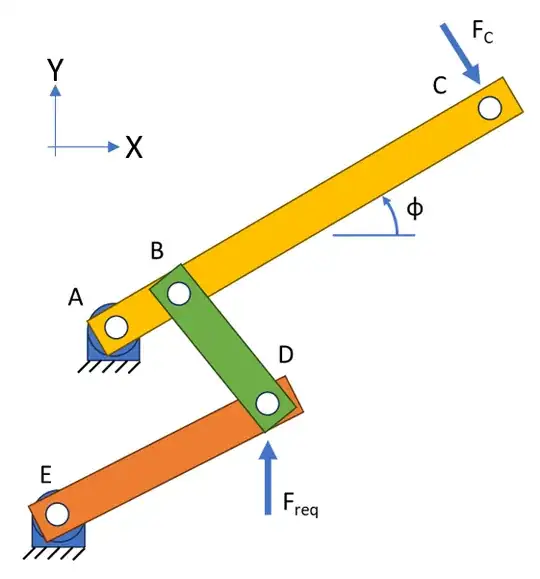
I have a four-bar linkage of known geometry (all angles, lengths, etc.) and I'm trying to solve for the required force to balance an input force.
Per this diagram, the input force (Fc, perpendicular to ABC) is known and the required force to counteract it (Freq, only in Y-axis) must be found. A and E are able to rotate, but not translate. I've tried different methods to solve for the force, but my results don't make sense once I plug-in some example values.
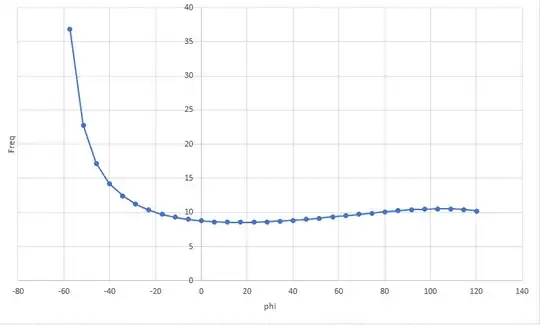
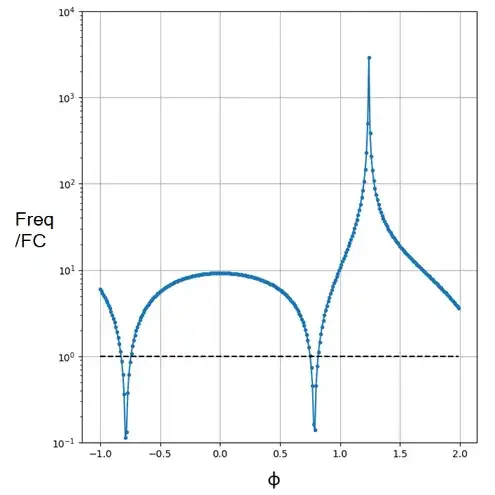
This plot shows the calculated ratio of Freq to Fc across a range of phi values. I wouldn't expect the ratio to suddenly change by several orders of magnitude, so I believe my solution is wrong.
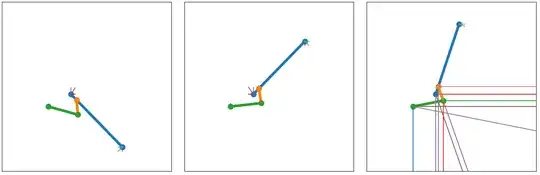
Edit: I've added plots of the three positions that result in the extreme points on the force plot, with forces shown as vector and X-Y components:
(AX=37, AY=50, EX=0, EY=30, LDE=50, LBD=24, LAB=13, LAC=120, phi=[-0.8, 0.8, 1.25])
I've evaluated the FBDs of each link:
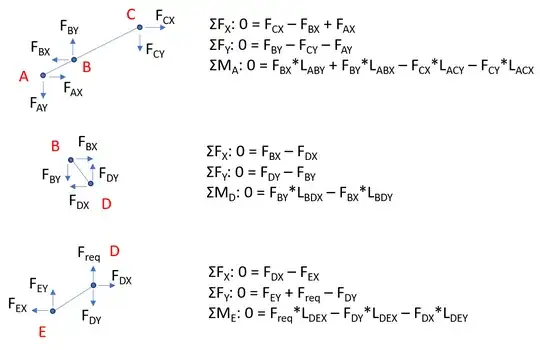
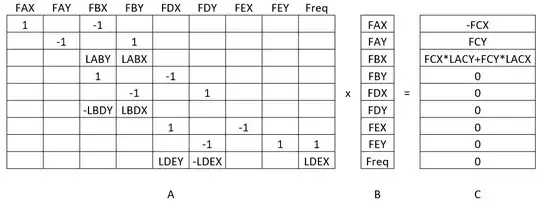
Then tried solving the equations directly and via matrix multiplication, but get the same result. I think the FBDs are where I must have gone wrong then. Can someone confirm, please?
My attempted matrix solution, for reference (blank cells are zeros):
Update: using SAM 8.4 I simulated the linkage and found the Freq for a 1N FC. Intuitively the curve makes sense because the spike on the left side is where AB approaches parallel with BD and the force is otherwise near LAC/LAB (~10):
Parameters: (AX=37, AY=45, EX=0, EY=30, LDE=50, LBD=25, LAB=13, LAC=120)
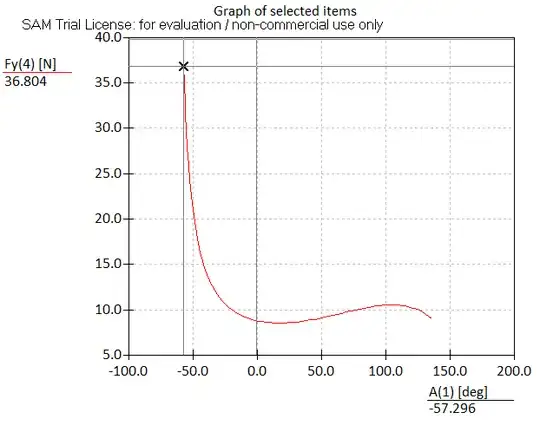
I'll assume that this represents an accurate curve to compare against.