2

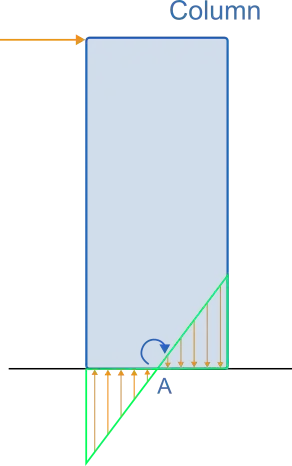
enter image description here

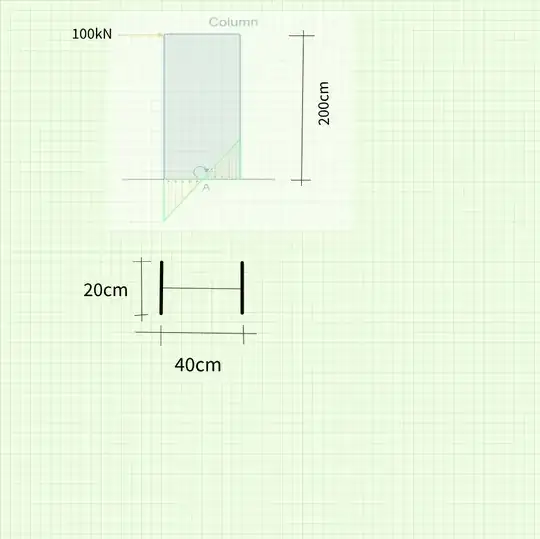
In the figure above, a horizontal singular force is applied to a column from its end point. If we examine the column with the finite element method, we see that there are tensile and compressive stresses at its base. If we can show these tension and pressure regressions along every point on the base, we will see that the concept we call moment is actually an effect caused by stresses. So my idea is an imaginary concept that emerges as a result of these tensions. For example, as civil engineers, we know that the bending of a plate is actually a phenomenon observed when tensile or compressive stresses exceed the yield strength of the material during bending. However, the figure below is a bar element model. It represents the same column and is a 1-dimensional element.

enter image description here

We cannot show tensile and compressive stresses simultaneously on a 1-dimensional column element. A single axial force can now be represented as either a tensile or compressive stress. However, since this is the point where the axial force is $0$ in the system, we show that the horizontal force produces a moment on the ground. If you ask what happens if we show both the moment and the axial force together in the first example, an error occurs. Because we would be showing the same concept twice. In your opinion, are there any shortcomings or mistakes regarding the subject? Because I have never seen such an article or article anywhere. It's a subject that has been bothering me for a long time. Since my university life, I am now in my master's degree.

Bilgehan Yılmaz
  • 41
  • 7
  • In the case of a thin rod, it has to be embedded into the foundation/soil to be able to transfer the moment at the base, the foundation will then produce a stress couple on the embedded part to counter the moment applied at the base. A free-standing/pinned rod can't take the lateral load. – r13 Aug 23 '24 at 01:48
  • 1
    One of the most detailed views of matter would be that it is just forces between particles. That is however extremely impractical, especially for engineers. So we invent imaginary concepts like moment, but also continuum, stress, temperature… Event your representations of a column can both be useful in specific circumstances instead of working with actual column with all of its details and imperfections. – Tomáš Létal Aug 23 '24 at 12:01
  • @TomášLétal Thank you, I think the same as you. Actually, the concept of moment is an important concept in the statics of objects that do not change shape. Because we don't care about internal forces there. – Bilgehan Yılmaz Aug 23 '24 at 14:18

2 Answers2

1

Torques are no more or less imaginary than forces. There are several conservation laws in our mathematical description of the world. One is linear momentum, which is governed by a force law; and another is angular momentum, which is governed by a moment law. These are 100% independent of each other. You can not describe conservation of angular momentum using forces. But we can construct multiple equivalent systems of forces and moments which satisfies both restrictions provided we have extras.

Consider a wheel in space and you pull on the rim. It's CG accelerates according to $F=m\times a$. But it also begins to spin about its CG according to $T=I\times \alpha$. We can predict the location of any point on the wheel by superposition of the two solutions.

Phil Sweet
  • 5,224
  • 10
  • 20
0

No, moment is not an imaginary concept, it is very real, and overlooking or underestimating it can be disastrous, as has happened some times, leading to numerous casualties.

In engineering moment is the effect of a force applied to a body that is stationary (hopefully) and causes stresses on that body that counter it and cause equilibrium.

For example, if you hold a shaft in your hands and try to bend it, it creates a couple of internal forces of tension and compression in the shaft that together cause a moment that is equal in magnitude and opposite in direction to the moment your hands impart on the shaft.

If we load a beam with a UDL, it creates a moment that has to be resisted by the interior beam moment, otherwise, it fails, potentially bringing the part of the building down.

For simplicity in engineering drawings, sometimes columns or beams are shown as lines, they are just symbols. A column or beam is stronger against the moment the wider it is. The very fundamental concept of a section's 2nd area moment is its geometry's contribution to its stiffness, in resisting external moments.

Edit

After the OP's comment,

Consider the column in your first shade of blue. It is a 200-cm-tall steel wide flange column with a 100kN force applied, as shown with a web thin enough that we can ignore it. As per the figure.

The flange on the right hand undergoes 500 kN compression, and the one on the left undergoes 500 kN tension.

$$F_C=F_T= \frac{100kN*2m}{0.4m}=500N$$

If these two forces were not acting as a couple, there would be no moment

But since they act together and try to turn the column, they produce 200kNm moment large enough to resist the overturning moment on the column of 200kNm. diagram

kamran
  • 23,517
  • 2
  • 22
  • 42