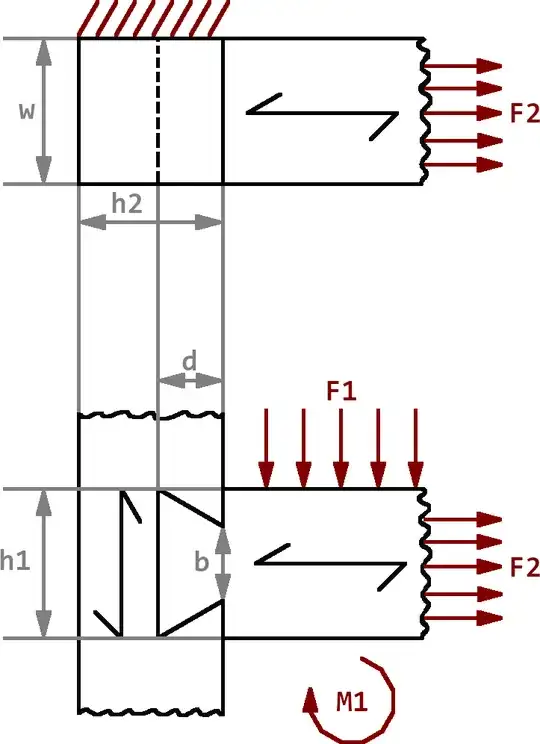
I am considering using a sliding dovetail joint (without glue) between two timber pieces: a vertical wall with a slot and a horizontal shelf with a tail. The thickness of the shelf is $h_1 = 18mm$, and the thickness of the wall is $h_2 = 25mm$ or $h_2 = 18mm$. The material is a scots pine glued panel (density $510\ kg/m^3$). The width of the shelf is $w = 600mm$. The shelf grain is directed towards the wall (horizontally, parallel to the force $F_2$). The wall grain is directed vertically (parallel to the force $F_1$). The depth of the tail penetration is $d$, and its bottleneck is $b$.
What is the optimal angle of the dovetail, and what forces can it theoretically withstand? For simplicity, we may consider the case when $F_2$ and $M_1$ are negligibly small and $F_1$ is the subject, and the case when $F_1$ and $M_1$ are negligibly small and $F_2$ is the subject. Also, I would like to know the dependency between the maximum momentum $M_1$ and depth $d$ and bottleneck width $b$.
My current understanding is as follows:
- $F_2$ will fight the shear strength of the shelf parallel to the grain in the case of small $b$ and the shear strength of the wall perpendicular to the grain in the case of small $d$
- Analogously, $F_1$ will fight the shear strength of the shelf perpendicular to the grain if $b$ is small and the shear strength of the wall parallel to the grain if $b$ is significant.
- $M_1$ will compete with the tensile strength of the wall parallel to the grain if $d \approx h_2$, with the bending strength of the shelf if $b$ is small, or with the bending strength of the wall if $d$ is small (using the tail end as a lever).
However, I am unsure whether it is right and how to apply the strength values to the dovetail's geometry to calculate ultimate and design stresses.