How was the length of the damper calculated in this figure?

Question

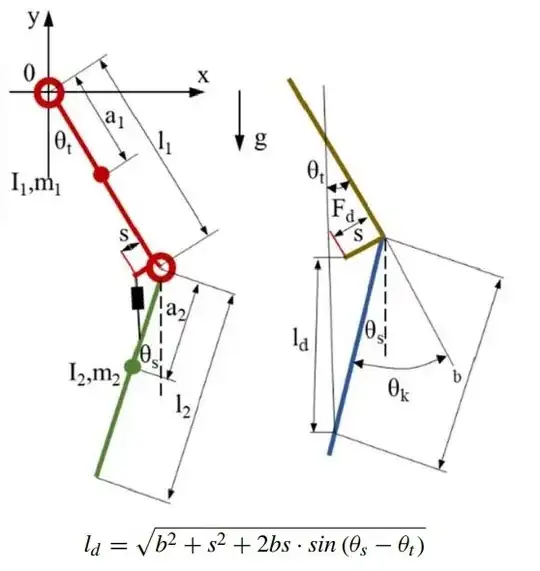
I was reading this research and tried to calculate the length of the damper but couldn't figure out how. tried using the Law of Cosines but ended up with a different result.

Answer 1

you are right.

Lets call the second point at the center of the red circle E and the point of intersection of it with ld, F. so $ \ EF = a_2$

Using the law of cosines and recognizing that the angle between the two sides is$\ 90 - \theta_ k$ or $\ 90 - \theta_t - \theta_s$

$$ld^2 = S^2 +a_2^2 - 2 S a_2 \ cos(90- \theta_t - \theta_s) $$ so $$ld = \sqrt{S^2 +a_2^2 - 2 S a_2 \ cos(90- \theta_t - \theta_s)}$$

Edit

After OP comment

yes:

if you look at the diagram the $cos(\theta_t)$ is positive, but $cos(\theta_s)$ is negative. and we know two complementary angles have

$$sin\alpha= \pm cos (90-\alpha)= \pm sin(\theta_s- \theta_t)= sin(\theta_s-\theta_t)$$

I skipped a couple of steps. I am confident you know it.

I guess this format would be more convenient for authors' future calculations.