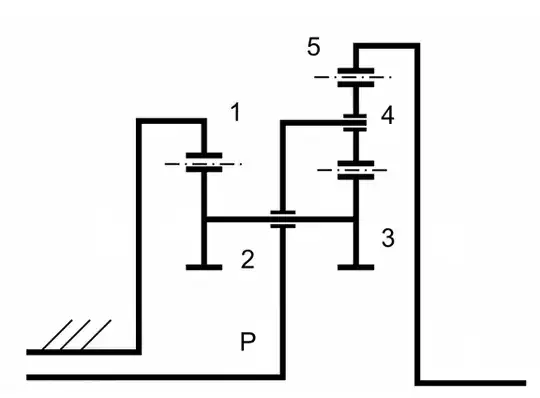
In the scheme there is a planetary gearset. I Know: Z1 = 102, Z2 = 11; Z3 = 13; Z4 = 19; Z5 = 152 and the angular velocity of gear 5 is 28 rad/s.
I use the typical reletion: $ \frac{\omega _{5} - \omega _{p}}{\omega _{1} - \omega _{p}} = \prod \tau _{i}= \frac{Z_{1}}{Z_2}- \frac{Z_3}{Z_5}. $
I think that $ \omega_1=0 $ (based on the picture) and also that the gear 4 could be a free gear.
I don't know what I have to think to put the correct sign (+ or -) when i divide the teeth number and also how to see if a gear is free.
I have to find $ \omega_p $.
Image source: me, i have copied it during a lesson.