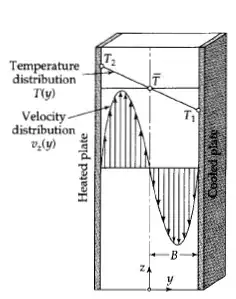
Problem: Consider two walls separated by distance $2B$ with a fluid of density $\rho$ and viscosity $\mu$ located between the vertical walls. The left wall (at $y=-B$) is at temperature $T_2$ and the right wall (at $y=B$) is at $T_1$. Additionally assume $\Delta T = T_2-T_1>0$ is small (that is, neglect $(\Delta T)^2$ terms). Find velocity flow of the fluid. Below is a diagram: $\hspace{3cm}$
This problem has been discussed in depth in the book "Transport phenomenon, 2nd ed" by Bird, Stewart, Lightfoot in section 10.9. In what follows, I will refer to a few equations in this section of the book which I understand, and then mark the equation where I am unable to make progress. In equation 10.9-4, from an energy the temperature profile $T(y) = \overline{T}-\frac{1}{2}\Delta T \frac{y}{B}$ is computed where $\overline{T} = \frac{T_1+T_2}{2}.$ Next, after performing a momentum balance, the governing equation 10.9-5 $$\mu \frac{d^2 v_z}{dy^2} = \frac{dp}{dz} + \rho g$$ is obtained where $v_z$ is the velocity component in $z$ direction (the only component which is non-zero), $p$ is the pressure, and $\rho$ is the density. To simply the density term, perform a taylor expansion of $\rho$ at $\overline{T}$ to obtain equation 10.9-6 $$ \rho = \overline{\rho}-\overline{\rho} \overline{\beta}(T-\overline{T})$$ Substituting equation 10.9-6 and temperature profile in the governing equation, the book gets to equation 10.9-12 $$ v_z(y)=\frac{(\bar{\rho} g \bar{\beta} \Delta T) B^2}{12 \mu}\left[\left(\frac{y}{B}\right)^3-\left(\frac{y}{B}\right)\right]+\frac{B^2}{2 \mu}\left(\frac{d p}{d z}+\bar{\rho} g\right)\left[\left(\frac{y}{B}\right)^2-1\right],$$ which I was able to understand. The book now claims that $\frac{dp}{dz} = -\overline{\rho}g$ using the mass balance equation $\int_{-B}^{B} \rho v_z dy = 0$. I performed the computation and got the following: Define $c_1 = \frac{(\bar{\rho} g \bar{\beta} \Delta T) B^2}{12 \mu}$ and $c_2 = \frac{B^2}{2 \mu}\left(\frac{d p}{d z}+\bar{\rho} g\right)$, then \begin{align*} &\int_{-B}^{B} \rho v_z dy \overset{w=y/B}{=} B\int_{-1}^{1} \left(\overline{\rho} + \frac{1}{2}\overline{\rho} \overline{\beta} \Delta T w \right))(c_1 (w^3-w)+c_2(w^2-1))dw=0,\\ &\implies B\overline{\rho} c_2\int_{-1}^{1} w^2-1 dw + c_1\frac{1}{2}B\overline{\rho} \overline{\beta} \Delta T \int_{-1}^{1} w^4-w^2 dw=0,\\ &\implies 2c_2 + \overline{\beta} \Delta T \frac{c_1}{5} = 0. \end{align*} From this we don't get the required result : $c_2 = 0$, that is, $\frac{d p}{d z}=-\bar{\rho} g$. Am I doing something incorrectly?