Why does the state transition matrix of a Discrete-PI controller have a real eigenvalue at 1 when $K_I = 0$?

Question

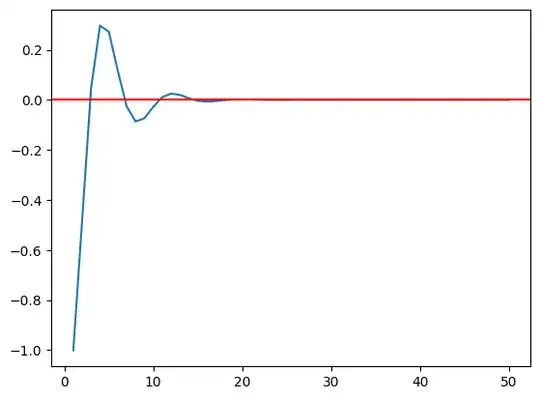
I am working with the state-space representation of a PI controller for a system with a 1-step delay. When the integral gain $K_I$ is set to zero, the controller effectively becomes proportional-only. Under these conditions, I notice that the state transition matrix always has a real eigenvalue at $1 + 0j$ even the $K_P$ lower than ultimate gain and the system do converge ($e$ converge to 0).

Base equation

$$ []=[−1]−[−2] $$ $$ []=[−1]+_0 []+_1 [−1] $$ $$ []=(_0+_1 )[−1]+[−1]−_0 [−2] $$

State vector:

$$ x[k] = \begin{bmatrix} e[k] \\ u[k] \\ u[k-1] \end{bmatrix} $$

State transition equation:

$$ x[k] = \mathbf{A} x[k-1] $$ where: $$ \mathbf{A} = \begin{bmatrix} 1 & 0 & -k \\ (b_0 + b_1) & 1 & -b_0 k \\ 0 & 1 & 0 \end{bmatrix} $$ $$ b_0 = K_P+K_iT/2 $$ $$ b_1 = -K_P+K_iT/2 $$ When $K_I = 0$, the coefficients simplify to $b_1 = 0$, and the eigenvalue $1$ always appears.

Why does this happen, and what is the mathematical or control-theoretic reasoning behind this eigenvalue being $1$ when there is no integral gain?

Pole location on z-plane

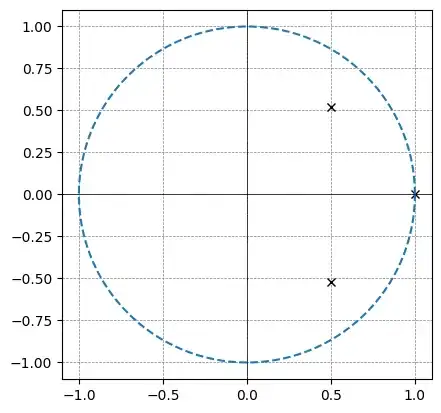I used numpy.linalg.eig to find eigenvalue od state stransition matrix.

Unit step response

Answer 1

I use python and matrix eigenvalue

The the integration / accumulation occurs in the equation $[]=[−1]−[−2]$. This appears in the first row of the matrix $A$ and is not affected by either the gain $K1$ or $K2$. Those gains only say if the output of the integrator influences the state $u$.

The system dynamics (represented by $A$) still contains the eigen value of $1+0i$. It is just that it is "un observable" at the output $u[k]$. If you model the input and output matrices $B$ and $C$ for the system and do the Python equivalent of "pzmap()" from Matlab / GNU Octave, you will be able to notice that the pole / eigen value at $1+0i$ is cancelled exactly by a "zero" at 1+0i.